Advertisements
Advertisements
प्रश्न
Solve graphically : 5x – 3y ≤ 0
उत्तर
Consider the line whose equation is 5x – 3y = 0. The constant term is zero, therefore this line is passing through the origin.
∴ one point on the line is the origin O = (0, 0).
To find the other point, we can give any value of x and get the corresponding value of y.
Put x = 3, we get 15 – 3y = 0, i.e. y = 5
∴ A = (3, 5) is another point on the line. Draw the line OA.
To find the solution set, we cannot check O(0,0), as it is already on the line. We can check any other point which is not on the line.
Let us check the point (1, – 1).
When x = 1, y = – 1 then 5x – 3y = 5 + 3 = 8 which is neither less nor equal to zero.
∴ 5x – 3y `cancel<=` 0 in this case.
Hence (1, – 1) will not lie in the required region.
Therefore the required region is the upper side which is shaded in the graph.
This is the solution set of 5x – 3y ≤ 0.
APPEARS IN
संबंधित प्रश्न
Solve graphically : y ≥ 0
Solve graphically : x ≤ 0
Solve graphically : y ≤ 0
Solve graphically: x ≤ 0 and y ≥ 0
Solve graphically : x ≤ 0 and y ≤ 0
Solve graphically : x ≥ 0 and y ≤ 0.
Solve graphically: 2x – 3 ≥ 0
Solve graphically : 5y + 3 ≤ 0
Solve graphically : 2x – 5y ≥10
Solve graphically: 3x + 2y ≥ 0
Solve graphically : 2x + y ≥ 2 and x – y ≤ 1
Solve graphically : x – y ≤ 2 and x + 2y ≤ 8
Solve graphically : x + y ≥ 6 and x + 2y ≤ 10
Solve graphically : 2x + 3y≤ 6 and x + 4y ≥ 4
Solve graphically : 2x + y ≥ 5 and x – y ≤ 1
The corner points of the feasible solutions are (0, 0) (3, 0) (2, 1) (0, 7/3) the maximum value of Z = 4x + 5y is
The half plane represented by 4x + 3y >14 contains the point
The value of objective function is maximum under linear constraints
If a corner point of the feasible solutions are (0, 10) (2, 2) (4, 0) (3, 2) then the point of minimum Z = 3x + 2y is
A solution set of the inequality x ≥ 0
Show the solution set of inequations 4x – 5y ≤ 20 graphically
If the point (x1, y1) satisfies px - qy < 13, then the solution set represented by the inequation is ______
Let p and q be the statements:
p: 3x3 + 8y3 ≥ 15, q: 5x + 2y < 11
Then, which of the following is true?
The maximum value of z = 7x + 6y.
Subject to the constraints x ≤ 45, y ≤ 55 and x ≥ 0, y ≥ 0 is ______.
Region represented by the inequalities x ≥ 0, y ≤ 0 is ______.
If S1 and S2 are respectively the sets of local minimum and local maximum points of the function, f(x) = 9x4 + 12x3 - 36x2 + 25, x ∈ R, then ______
Determine the system of linear equation for which the solution set is the shaded region in the following figure ______.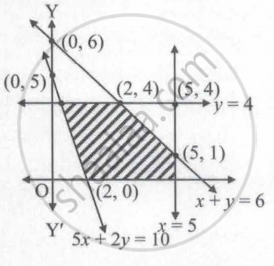
The set of real x satisfying the inequality `(5 - 2x)/3 ≤ x/6 - 5` is [a, ∞). The value of ‘a’ is ______.
Which of the following linear inequalities satisfy the shaded region of the given figure?
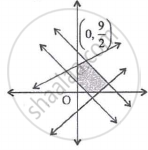
The objective function of LPP defined over the convex set attains it optimum value at ______.
