Advertisements
Advertisements
प्रश्न
Solve the following linear programming problems by graphical method.
Maximize Z = 20x1 + 30x2 subject to constraints 3x1 + 3x2 ≤ 36; 5x1 + 2x2 ≤ 50; 2x1 + 6x2 ≤ 60 and x1, x2 ≥ 0.
उत्तर
Given that 3x1 + 3x2 ≤ 36
Let 3x1 + 3x2 = 36
| x1 | 0 | 12 |
| x2 | 12 | 0 |
Also given that 5x1 + 2x2 ≤ 50
Let 5x1 + 2x2 = 50
| x1 | 0 | 10 |
| x2 | 25 | 0 |
3x1 + 3x2 = 36
x1 + x2 = 12 ……….(1)
5x1 + 2x2 = 50 ………(2)
2x1 + 2x2 = 24 ....[(1) × 2]
− − −
−3x1 = − 6
x1 = 2
Substituting x1 = 2 in (1) we get
2+ x2 = 12
x2 = 6
Also given that 2x1 + 6x2 ≤ 60
Let 2x1 + 6x2 = 60
x1 + 3x2 = 30
| x1 | 0 | 30 |
| x2 | 10 | 0 |
x1 + x2 = 12 …….(1)
x1 + 3x2 = 30 …….(2)
– 2x2 = – 18 ......[Equation (1) – (2)]
x2 = 9
x2 = 9 substitute in (1)
x1 + x2 = 12
x1 + 9 = 12
x1 = 12 – 9
x1 = 3
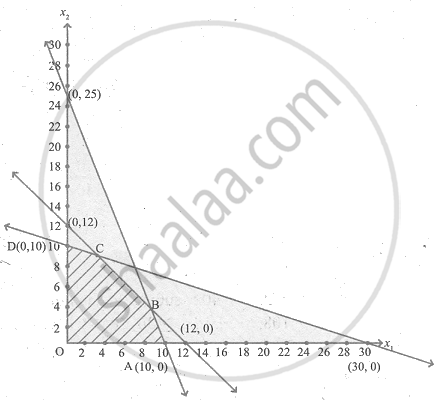
The feasible region satisfying all the given conditions is OABCD.
The co-ordinates of the comer points are
| Corner points | Z = 20x1 + 30x2 |
| O(0, 0) | 0 |
| A(10, 0) | 200 |
| B(2, 6) | 220 |
| C(3, 9) | 330 |
| D(0, 10) | 300 |
The maximum value of Z occurs at C(3, 9)
∴ The optimal solution is x1 = 3, x2 = 9 and Zmax = 330
APPEARS IN
संबंधित प्रश्न
Select the appropriate alternatives for each of the following question:
The value of objective function is maximum under linear constraints
Solve the following LPP:
Maximize z =60x + 50y subject to
x + 2y ≤ 40, 3x + 2y ≤ 60, x ≥ 0, y ≥ 0.
A printing company prints two types of magazines A and B. The company earns ₹ 10 and ₹ 15 on magazines A and B per copy. These are processed on three machines I, II, III. Magazine A requires 2 hours on Machine I, 5 hours on Machine II and 2 hours on Machine III. Magazine B requires 3 hours on Machine I, 2 hours on Machine II and 6 hours on Machine III. Machines I, II, III are available for 36, 50, 60 hours per week respectively. Formulate the Linear programming problem to maximize the profit.
A company manufactures two types of fertilizers F1 and F2. Each type of fertilizer requires two raw materials A and B. The number of units of A and B required to manufacture one unit of fertilizer F1 and F2 and availability of the raw materials A and B per day are given in the table below:
| Raw Material\Fertilizers | F1 | F2 | Availability |
| A | 2 | 3 | 40 |
| B | 1 | 4 | 70 |
By selling one unit of F1 and one unit of F2, company gets a profit of ₹ 500 and ₹ 750 respectively. Formulate the problem as L.P.P. to maximize the profit.
State whether the following statement is True or False:
Objective function of LPP is a relation between the decision variables
In the given graph the coordinates of M1 are

Solve the following LP.P.
Maximize z = 13x + 9y,
Subject to 3x + 2y ≤ 12,
x + y ≥ 4,
x ≥ 0,
y ≥ 0.
Shamli wants to invest ₹ 50, 000 in saving certificates and PPF. She wants to invest atleast ₹ 15,000 in saving certificates and at least ₹ 20,000 in PPF. The rate of interest on saving certificates is 8% p.a. and that on PPF is 9% p.a. Formulation of the above problem as LPP to determine maximum yearly income, is ______.
Sketch the graph of the following inequation in XOY co-ordinate system.
x + y ≤ 0
Sketch the graph of the following inequation in XOY co-ordinate system.
2y - 5x ≥ 0
