Advertisements
Advertisements
प्रश्न
State whether the following statement is True or False:
Of all the points of feasible region, the optimal value is obtained at the boundary of the feasible region
पर्याय
True
False
उत्तर
True
APPEARS IN
संबंधित प्रश्न
Solve the following L.P.P. by graphical method:
Minimize: Z = 6x + 2y subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0.
Choose the correct alternative:
The value of objective function is maximize under linear constraints.
Choose the correct alternative :
The maximum value of z = 5x + 3y. subject to the constraints
Choose the correct alternative :
The maximum value of z = 10x + 6y, subjected to the constraints 3x + y ≤ 12, 2x + 5y ≤ 34, x ≥ 0, y ≥ 0 is.
Choose the correct alternative:
The maximum value of Z = 3x + 5y subjected to the constraints x + y ≤ 2, 4x + 3y ≤ 12, x ≥ 0, y ≥ 0 is
Choose the correct alternative:
The corner points of feasible region for the inequations, x + y ≤ 5, x + 2y ≤ 6, x ≥ 0, y ≥ 0 are
Choose the correct alternative:
The corner points of the feasible region are (4, 2), (5, 0), (4, 1) and (6, 0), then the point of minimum Z = 3.5x + 2y = 16 is at
State whether the following statement is True or False:
If LPP has two optimal solutions, then the LPP has infinitely many solutions
State whether the following statement is True or False:
A convex set includes the points but not the segment joining the points
If the feasible region is bounded by the inequations 2x + 3y ≤ 12, 2x + y ≤ 8, 0 ≤ x, 0 ≤ y, then point (5, 4) is a ______ of the feasible region
A chemist has a compound to be made using 3 basic elements X, Y, Z so that it has at least 10 litres of X, 12 litres of Y and 20 litres of Z. He makes this compound by mixing two compounds (I) and (II). Each unit compound (I) had 4 litres of X, 3 litres of Y. Each unit compound (II) had 1 litre of X, 2 litres of Y and 4 litres of Z. The unit costs of compounds (I) and (II) are ₹ 400 and ₹ 600 respectively. Find the number of units of each compound to be produced so as to minimize the cost
Minimize Z = 2x + 3y subject to constraints
x + y ≥ 6, 2x + y ≥ 7, x + 4y ≥ 8, x ≥ 0, y ≥ 0
Solve the LPP graphically:
Minimize Z = 4x + 5y
Subject to the constraints 5x + y ≥ 10, x + y ≥ 6, x + 4y ≥ 12, x, y ≥ 0
Solution: Convert the constraints into equations and find the intercept made by each one of it.
| Inequations | Equations | X intercept | Y intercept | Region |
| 5x + y ≥ 10 | 5x + y = 10 | ( ___, 0) | (0, 10) | Away from origin |
| x + y ≥ 6 | x + y = 6 | (6, 0) | (0, ___ ) | Away from origin |
| x + 4y ≥ 12 | x + 4y = 12 | (12, 0) | (0, 3) | Away from origin |
| x, y ≥ 0 | x = 0, y = 0 | x = 0 | y = 0 | 1st quadrant |
∵ Origin has not satisfied the inequations.
∴ Solution of the inequations is away from origin.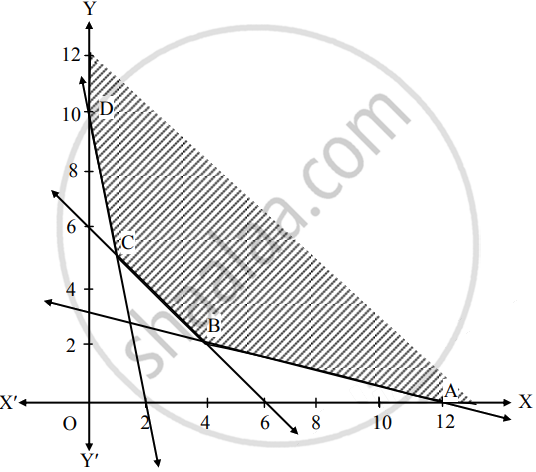
The feasible region is unbounded area which is satisfied by all constraints.
In the figure, ABCD represents
The set of the feasible solution where
A(12, 0), B( ___, ___ ), C ( ___, ___ ) and D(0, 10).
The coordinates of B are obtained by solving equations
x + 4y = 12 and x + y = 6
The coordinates of C are obtained by solving equations
5x + y = 10 and x + y = 6
Hence the optimum solution lies at the extreme points.
The optimal solution is in the following table:
| Point | Coordinates | Z = 4x + 5y | Values | Remark |
| A | (12, 0) | 4(12) + 5(0) | 48 | |
| B | ( ___, ___ ) | 4( ___) + 5(___ ) | ______ | ______ |
| C | ( ___, ___ ) | 4( ___) + 5(___ ) | ______ | |
| D | (0, 10) | 4(0) + 5(10) | 50 |
∴ Z is minimum at ___ ( ___, ___ ) with the value ___
A linear function z = ax + by, where a and b are constants, which has to be maximised or minimised according to a set of given condition is called a:-
Maximised value of z in z = 3x + 4y, subject to constraints : x + y ≤ 4, x ≥ 0. y ≥ 0
If z = 200x + 500y .....(i)
Subject to the constraints:
x + 2y ≥ 10 .......(ii)
3x + 4y ≤ 24 ......(iii)
x, 0, y ≥ 0 ......(iv)
At which point minimum value of Z is attained.
Shraddho wants to invest at most ₹ 25,000/- in saving certificates and fixed deposits. She wants to invest at least ₹ 10,000/- in saving certificate and at least ₹ 15,000/- in fixed deposits. The rate of interest on saving certificate is 5% and that on fixed deposits is 7% per annum. Formulate the above problem as LPP to determine maximum income yearly.
