Advertisements
Advertisements
प्रश्न
The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Ani and Biju is twice as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju
उत्तर
The difference between the ages of Biju and Ani is 3 years. Either Biju is 3 years older than Ani or Ani is 3 years older than Biju. However, it is obvious that in both cases, Ani’s father’s age will be 30 years more than that of Cathy’s age.
Let the age of Ani and Biju be x and y years respectively.
Therefore, age of Ani’s father, Dharam = 2 × x = 2x years
And age of Biju’s sister Cathy = `y/2` year
By using the information given in the question,
Case (I) When Ani is older than Biju by 3 years,
x − y = 3 (i)
`2x -y/2 = 30`
4x − y = 60 (ii)
Subtracting (i) from (ii), we obtain
3x = 60 − 3 = 57
`x = 57/3 =19`
Therefore, age of Ani = 19 years And age of Biju = 19 − 3 = 16 years
Case (II) When Biju is older than Ani,
y − x = 3 (i)
`2x - y/2 = 30`
4x − y = 60 (ii)
Adding (i) and (ii), we obtain
3x = 63
x = 21
Therefore, age of Ani = 21 years And age of Biju = 21 + 3 = 24 years
APPEARS IN
संबंधित प्रश्न
Solve `\frac { 2 }{ x } + \frac { 1 }{ 3y } = \frac { 1}{ 5 }; \frac { 3 }{ x } + \frac { 2 }{ 3y } = 2` and also find ‘a’ for which y = ax – 2
Solve the following pairs of equations by reducing them to a pair of linear equations
`2/sqrtx +3/sqrty = 2`
`4/sqrtx - 9/sqrty = -1`
Formulate the following problems as a pair of equations, and hence find their solutions:
2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.
Draw the graphs of the equations 5x − y = 5 and 3x − y = 3. Determine the coordinates of the vertices of the triangle formed by these lines and the y axis.
Solve the following pair of linear equations
ax + by = c
bx + ay = 1 + c
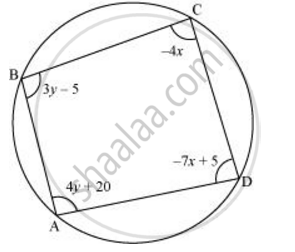
ABCD is a cyclic quadrilateral finds the angles of the cyclic quadrilateral.
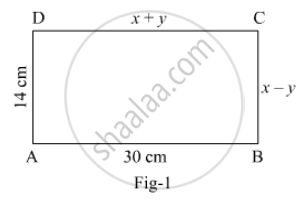
In Fig. 1, ABCD is a rectangle. Find the value of x and y.
A two-digit number is 4 more than 6 times the sum of its digits. If 18 is subtracted from the number, the digits are reversed. Find the number.
A two-digit number is such that the product of its digits is 20. If 9 is added to the number, the digits interchange their places. Find the number.
Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is `x/y`
If the numerator is multiplied by 2 and the denominator is reduced by 5, the fraction becomes `6/5`. Thus, we have
`(2x)/(y-5)=6/5`
`⇒ 10x=6(y-5)`
`⇒ 10x=6y-30`
`⇒ 10x-6y+30 =0`
`⇒ 2(5x-3y+15)=0`
`⇒ 5x - 3y+15=0`
If the denominator is doubled and the numerator is increased by 8, the fraction becomes `2/5`. Thus, we have
`(x+8)/(2y)=2/5`
`⇒ 5(x+8)=4y`
`⇒ 5x+40=4y`
`⇒ 5x-4y+40=0`
So, we have two equations
`5x-3y+15=0`
`5x-4y+40=0`
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have
`x/((-3)xx40-(-4)xx15)=-y/(5xx40-5xx15)=1/(5xx(-4)-5xx(-3))`
`⇒ x/(-120+60)=(-y)/(200-75)=1/(-20+15)`
`⇒x/(-60)=-y/125``=1/-5`
`⇒ x= 60/5,y=125/5`
`⇒ x=12,y=25`
Hence, the fraction is `12/25`
