Advertisements
Advertisements
प्रश्न
The boilers are used in thermal power plants to store water and then used to produce steam. One such boiler consists of a cylindrical part in middle and two hemispherical parts at its both ends.
Length of the cylindrical part is 7 m and radius of cylindrical part is `7/2` m.
Find the total surface area and the volume of the boiler. Also, find the ratio of the volume of cylindrical part to the volume of one hemispherical part.

उत्तर
Given that,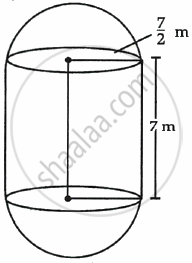
Length of cylindrical part = 7 m
Radius of cylindrical part = `7/2` m
Total surface area of figure = 2πrh + 2(2πr2)
= `2π[7/2 xx 7 + 2 xx (7/2)^2]`
= 308 m2
Volume of boiler = Volume of cylindrical part + Volume of two hemispherical parts
= `πr^2h + (4/3)πr^3`
= `π(7/2)^2 xx (7) + (4/3)π(7/2)^3`
= 269.5 + 179.66
= 449.167 m3
Required Ratio = `"Volume of cylindrical part"/"Volume of one hemispherical part"`
= `269.5/89.83`
= 3
संबंधित प्रश्न
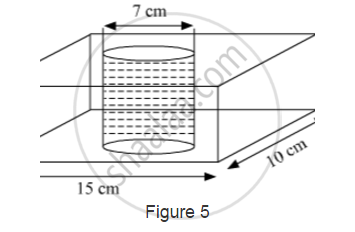
In Fig. 5, from a cuboidal solid metallic block, of dimensions 15cm ✕ 10cm ✕ 5cm, a cylindrical hole of diameter 7 cm is drilled out. Find the surface area of the remaining block [Use
`pi=22/7`]
A cylindrical bucket 28 cm in diameter and 72 cm high is full of water. The water is emptied into a rectangular tank 66 cm long and 28 cm wide. Find the height of the water level in the tank.
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid.
From a cubical piece of wood of side 21 cm, a hemisphere is carved out in such a way that the diameter of the hemisphere is equal to the side of the cubical piece. Find the surface area and volume of the remaining piece.
If the areas of three adjacent faces of a cuboid are x, y and z, respectively, the volume of the cuboid is ______.
If the volumes of a cube is 1728 cm³, the length of its edge is equal to ______.
Two cubes each of volume 8 cm³ are joined end to end, then the surface area of the resulting cuboid is ______.
A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. The total surface area of the combined solid is `pir [sqrt(r^2 + h^2) + 3r + 2h]`.
There are two identical solid cubical boxes of side 7 cm. From the top face of the first cube a hemisphere of diameter equal to the side of the cube is scooped out. This hemisphere is inverted and placed on the top of the second cube’s surface to form a dome. Find
- the ratio of the total surface area of the two new solids formed
- volume of each new solid formed.
3 cubes each of 8 cm edge are joined end to end. Find the total surface area of the cuboid.
