Advertisements
Advertisements
प्रश्न
The cost of manufacturing x articles is Rs.(50 + 3x). The selling price of x articles is Rs. 4x.
On a graph sheet, with the same axes, and taking suitable scales draw two graphs, first for the cost of manufacturing against no. of articles and the second for the selling price against the number of articles.
Use your graph to determine:
The profit or loss made when (a) 30 (b) 60 articles are manufactured and sold.
उत्तर
Given that C.P. is 50 + 3x
Table of C.P.
| X | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| C.P. | 50 | 80 | 110 | 140 | 170 | 200 | 230 |
and S.P. = 4x
∴ Table of S.P.
| X | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| S.P. | 0 | 40 | 80 | 120 | 160 | 200 | 240 |
Now plot the points on a graph and we get the following required graph:
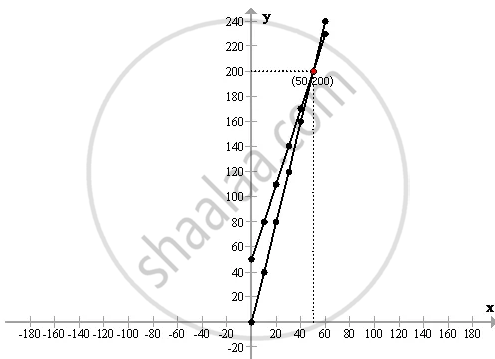
(a)
On article 30,
C.P. = Rs.140 and S.P. = 120
Therefore Loss = 140 - 120 = Rs. 20
(b)
On article 60,
C.P.= Rs. 230 and S.P.= Rs. 240
Therefore Profit = 240 - 230 = Rs.10
APPEARS IN
संबंधित प्रश्न
The sides of a triangle are given by the equations y - 2 = 0; y + 1 = 3 (x - 2) and x + 2y = 0.
Find, graphically :
(i) the area of a triangle;
(ii) the coordinates of the vertices of the triangle.
Solve graphically, the following equations.
x + 2y = 4; 3x - 2y = 4.
Take 2 cm = 1 unit on each axis.
Also, find the area of the triangle formed by the lines and the x-axis.
Solve the following equations graphically :
x + 4y + 9 = 0
3y = 5x - 1
Solve the following equations graphically :
x - 2y = 2
`x/(2) - y` = 1
Solve the following system of linear equations graphically :
4x - 5y - 20 = 0
3x + 3y - 15 = 0
Determine the vertices of the triangle formed by the lines, represented by the above equations and the y-axis.
Solve the following system of equations graphically
x - y + 1 = 0
4x + 3y = 24
Draw the graph of the following equations :
3x + 2y + 6 = 0
3x + 8y - 12 = 0
Also, determine the co-ordinates of the vertices of the triangle formed by these lines and x-axis.
Solve graphically
3x + 2y = 4, 9x + 6y – 12 = 0
Solve graphically
y = 2x + 1, y + 3x – 6 = 0
Solve graphically
x = −3, y = 3
