Advertisements
Advertisements
Question
The cost of manufacturing x articles is Rs.(50 + 3x). The selling price of x articles is Rs. 4x.
On a graph sheet, with the same axes, and taking suitable scales draw two graphs, first for the cost of manufacturing against no. of articles and the second for the selling price against the number of articles.
Use your graph to determine:
The profit or loss made when (a) 30 (b) 60 articles are manufactured and sold.
Solution
Given that C.P. is 50 + 3x
Table of C.P.
| X | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| C.P. | 50 | 80 | 110 | 140 | 170 | 200 | 230 |
and S.P. = 4x
∴ Table of S.P.
| X | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| S.P. | 0 | 40 | 80 | 120 | 160 | 200 | 240 |
Now plot the points on a graph and we get the following required graph:
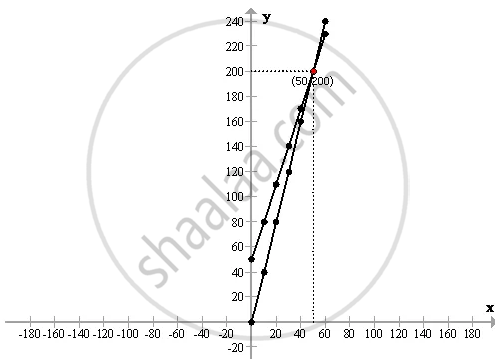
(a)
On article 30,
C.P. = Rs.140 and S.P. = 120
Therefore Loss = 140 - 120 = Rs. 20
(b)
On article 60,
C.P.= Rs. 230 and S.P.= Rs. 240
Therefore Profit = 240 - 230 = Rs.10
APPEARS IN
RELATED QUESTIONS
Find graphically, the vertices of the triangle whose sides have the equations 2y - x = 8; 5y - x = 14 and y - 2x = 1 respectively. Take 1 cm = 1 unit on both the axes.
Using the same axes of co-ordinates and the same unit, solve graphically :
x + y = 0 and 3x - 2y = 10.
(Take at least 3 points for each line drawn).
The course of an enemy submarine, as plotted on rectangular co-ordinate axes, gives the equation 2x + 3y = 4. On the same axes, a destroyer's course is indicated by the graph x - y = 7. Use the graphical method to find the point at which the paths of the submarine and the destroyer intersect?
Solve the following equations graphically :
x + 4y + 9 = 0
3y = 5x - 1
Solve the following equations graphically :
3y = 5 - x
2x = y + 3
Solve the following system of equations graphically:
2x = 23 - 3y
5x = 20 + 8y
Also, find the area of the triangle formed by these lines and x-axis in each graph.
Solve the following system of equations graphically:
6x - 3y + 2 = 7x + 1
5x + 1 = 4x - y + 2
Also, find the area of the triangle formed by these lines and x-axis in each graph.
Solve graphically
x + y = 7, x – y = 3
Solve graphically
y = 2x + 1, y + 3x – 6 = 0
Two cars are 100 miles apart. If they drive towards each other they will meet in 1 hour. If they drive in the same direction they will meet in 2 hours. Find their speed by using graphical method.
