Advertisements
Advertisements
Question
The course of an enemy submarine, as plotted on rectangular co-ordinate axes, gives the equation 2x + 3y = 4. On the same axes, a destroyer's course is indicated by the graph x - y = 7. Use the graphical method to find the point at which the paths of the submarine and the destroyer intersect?
Solution
2x + 3y = 4
⇒ x = `(4 - 3y)/(2)`
The table for 2x + 3y = 4 is
| X | -1 | -4 | 5 |
| Y | 2 | 4 | -2 |
x - y = 7
⇒ x = y + 7
The table for x - y = 7 is
| X | 5 | 11 | 9 |
| Y | -2 | 4 | 2 |
Now plot the points on a graph and we get the following required graph:
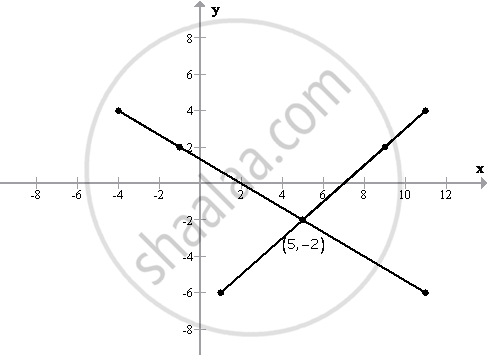
The point at which the paths of the submarine and the destroyer intersect are (5, -2)
APPEARS IN
RELATED QUESTIONS
Solve graphically the simultaneous equations given below. Take the scale as 2 cm = 1 unit on both the axes.
x - 2y - 4 = 0
2x + y = 3
Using the same axes of co-ordinates and the same unit, solve graphically :
x + y = 0 and 3x - 2y = 10.
(Take at least 3 points for each line drawn).
Solve the following equations graphically :
x = 4
`(3x)/(3) - y = 5`
Solve the following equations graphically :
x+ 2y - 7 = 0
2x - y - 4 = 0
Find graphically the vertices of the triangle, whose sides are given by 3y = x + 18, x + 7y = 22 and y + 3x = 26.
Solve the following system of linear equations graphically :
4x - 5y - 20 = 0
3x + 3y - 15 = 0
Determine the vertices of the triangle formed by the lines, represented by the above equations and the y-axis.
Solve the following system of equations graphically:
2x = 23 - 3y
5x = 20 + 8y
Also, find the area of the triangle formed by these lines and x-axis in each graph.
Solve graphically
3x + 2y = 4, 9x + 6y – 12 = 0
Solve graphically
`x/2 + y/4` = 1, `x/2 + y/4` = 2
Two cars are 100 miles apart. If they drive towards each other they will meet in 1 hour. If they drive in the same direction they will meet in 2 hours. Find their speed by using graphical method.
