Advertisements
Advertisements
Question
Solve the following system of equations graphically:
2x = 23 - 3y
5x = 20 + 8y
Also, find the area of the triangle formed by these lines and x-axis in each graph.
Solution
The given system of equations are 2x = 23 - 3y and 5x = 20 + 8y.
Now, 2x = 23 - 3y ....(i)
⇒ x = `(23 - 3y)/(2)`
Corresponding values of x and y can be tabulated as follows :
| x | 10 | 7 | 4 |
| y | 1 | 3 | 5 |
Plotting points (10, 1), (7, 3) and (4, 5) joining them, we get a line l1 which is the graph of equation (i).
Again, 5x = 20 + 8y ....(ii)
⇒ x = `(20x + 8y)/(5)`
Corresponding values of x and y can be tabulated as follows :
| x | 4 | 2.4 | 0.8 |
| y | 0 | -1 | -2 |
Plotting points (4, 0), (2.4, -1) and (0.8, -2) joining them, we get a line l2 which is the graph of equation (ii).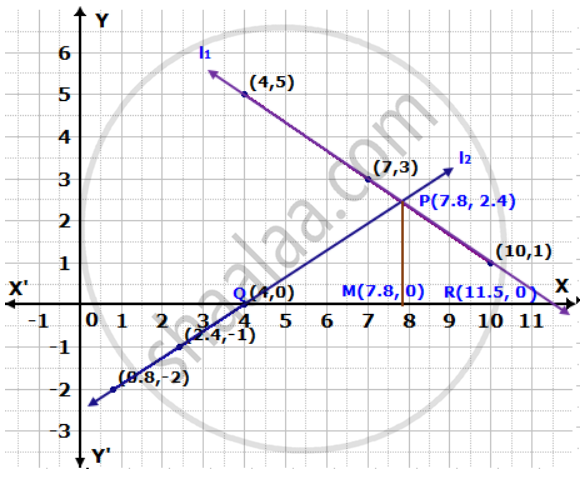
The two lines l1 and l2 intersect at a point P(7.8, 2.4).
∴ x = 7.8, y = 2.4 is the solution of the given system of equations.
Draw PM perpendicular from P to X-axis.
Now, PM = y-coordinate of P(7.8, 2.4)
⇒ PM = 2.4 units
QR = 11.5 - 4
= 7.5 units
∴ Area of ΔPQR
= `(1)/(2) xx "QR" xx "PM"`
= `(1)/(2) xx 7.5 xx 2.4`
= 9 sq. units.
APPEARS IN
RELATED QUESTIONS
The sides of a triangle are given by the equations y - 2 = 0; y + 1 = 3 (x - 2) and x + 2y = 0.
Find, graphically :
(i) the area of a triangle;
(ii) the coordinates of the vertices of the triangle.
Solve graphically, the following equations.
x + 2y = 4; 3x - 2y = 4.
Take 2 cm = 1 unit on each axis.
Also, find the area of the triangle formed by the lines and the x-axis.
The course of an enemy submarine, as plotted on rectangular co-ordinate axes, gives the equation 2x + 3y = 4. On the same axes, a destroyer's course is indicated by the graph x - y = 7. Use the graphical method to find the point at which the paths of the submarine and the destroyer intersect?
Solve the following equations graphically :
x = 4
`(3x)/(3) - y = 5`
Solve the following equations graphically :
`2 + (3y)/x = (6)/x`
`(6x)/y - 5 = (4)/y`
Find graphically the vertices of the triangle, whose sides have the equations 2y - x = 8, 5y -x = 14 and y = 2x - 1.
Solve the following system of linear equations graphically :
4x - 5y - 20 = 0
3x + 3y - 15 = 0
Determine the vertices of the triangle formed by the lines, represented by the above equations and the y-axis.
Draw the graph of the following equations :
3x + 2y + 6 = 0
3x + 8y - 12 = 0
Also, determine the co-ordinates of the vertices of the triangle formed by these lines and x-axis.
Solve the following system of equations graphically:
6x - 3y + 2 = 7x + 1
5x + 1 = 4x - y + 2
Also, find the area of the triangle formed by these lines and x-axis in each graph.
Solve graphically
`x/2 + y/4` = 1, `x/2 + y/4` = 2
