Advertisements
Advertisements
प्रश्न
The diameter of the moon is approximately one fourth of the diameter of the earth. Find the
ratio of their surface areas.
उत्तर
Let the diameter of the earth is d then, diameter of moon will be `d/4`
Radius of earth =`d/2`
Radius of moon = `2/4=d/8`
S.A of moon = `4πr(d/8)^2`
Surface area of earth = `4πr(d/2)^2`
Required ratio = `(4πr(d/8)^2)/(4πr(d/2)^2) = 4/64=1/16`
Thus, the required ratio of the surface areas is `1/16`.
APPEARS IN
संबंधित प्रश्न
Find the surface area of a sphere of radius 5.6 cm.
`["Assume "pi=22/7]`
The volume of one sphere is 27 times that of another sphere. Calculate the ratio of their :
- radii,
- surface areas.
If the number of square centimeters on the surface of a sphere is equal to the number of cubic centimeters in its volume, what is the diameter of the sphere?
A hemi-spherical bowl has negligible thickness and the length of its circumference is 198 cm. Find the capacity of the bowl.
If a sphere is inscribed in a cube, then the ratio of the volume of the sphere to the volume of the cube is
How many lead balls of radii 1 cm each can be made from a sphere of 8 cm radius?
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown.
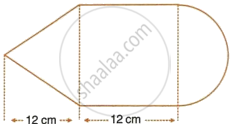
Calculate :
- the total surface area.
- the total volume of the solid and
- the density of the material if its total weight is 1.7 kg.
A spherical ball of radius 3 cm is melted and recast into three spherical balls. The radii of two of the balls are 1.5 cm and 2 cm. Find the diameter of the third ball.
The internal and external diameters of a hollow hemispherical vessel are 20 cm and 28 cm respectively. Find the cost to paint the vessel all over at ₹ 0.14 per cm2
A manufacturing company prepares spherical ball bearings, each of radius 7 mm and mass 4 gm. These ball bearings are packed into boxes. Each box can have maximum of 2156 cm3 of ball bearings. Find the:
- maximum number of ball bearings that each box can have.
- mass of each box of ball bearings in kg.
(use π = `22/7`)
