Advertisements
Advertisements
प्रश्न
The diameter of the wheel of a car is 70 cm. How many revolutions will it make to travel one kilometer?
उत्तर
The circumference of a circle is given by:
Circumference = π × Diameter.
Here, the diameter of the wheel is 70 cm. Substituting the value of π ≈ 3.1416
Circumference = 3.1416 × 70 = 219.91 cm
Since 1 km = 1000 m = 1000 × 100 = 100,000 cm, the total distance to be traveled is:
1 km = 100,000 cm.
The number of revolutions is the total distance divided by the circumference of the wheel:
Number of revolutions = `("Total distance")/("Circumference") = 100000/219.91`
Number of revolutions ≈ 454.74.
The wheel will make approximately 455 revolutions to travel 1 km.
APPEARS IN
संबंधित प्रश्न
Find the area of the square whose perimeter is 56 cm.
In the figure given below, find the area of shaded region: (All measurements are in cm)
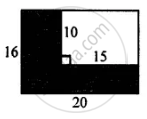
In the figure given below, find the area of shaded region: (All measurements are in cm)
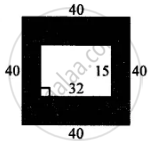
If the area of a rhombus is 112 cm2 and one of its diagonals is 14 cm, find its other diagonal.
Find the area of a triangle whose base is 30 cm and the height is 18 cm.
The area of a right-angled triangle is 160 cm2. If its one leg is 16 cm long, find the length of the other leg.
Find the area of an equilateral triangle whose each side is 16 cm. (Take `sqrt3`= 1.73)
The legs of a right-angled triangle are in the ratio 4 : 3 and its area is 4056 cm2. Find the length of its legs.
The ratio between the radius of two circles is 5 : 7. Find the ratio between their:
(i) circumference
(ii) areas
The ratio between the areas of two circles is 16 : 9. Find the ratio between their :
(i) radius
(ii) diameters
(iii) circumference
