Advertisements
Advertisements
प्रश्न
The ratio between the areas of two circles is 16 : 9. Find the ratio between their :
(i) radius
(ii) diameters
(iii) circumference
उत्तर
(i) Let radius of first circle = r1
and radius of second circle = r2
Given that ratio of the areas of circles = 16 : 9
⇒ `(π"r"_1^2)/(π"r"_2^2)=16/9`
⇒ `(π"r"_1^2)/(π"r"_2^2)=4^2/3^2`
⇒ `("r"_1)/("r"_2)=4/3`
(ii) Let the diameter of first circle = d1
and diameter of second circle = d2
Since, we know that diameter = 2 × radius
∴ d1 = 2 × r1 = 2 × 4x = 8x
and d2 = 2 × r2 = 2 × 3x = 6x
Now, the ratio between the diameter of two circles = d1 : d2
= 8x : 6x = 4 : 3
(iii) Now, consider the ratio of circumference of the circles
= `(2π"r"_1)/(2π"r"_2)="r"_1/"r"_2=4/3`
∴ The ratio between the circumference of two circles = 4 : 3
APPEARS IN
संबंधित प्रश्न
In the figure given below, find the area of shaded region: (All measurements are in cm)
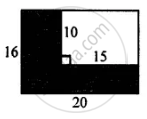
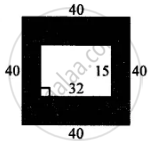
In the figure given below, find the area of shaded region: (All measurements are in cm)
One side of a parallelogram is 20 cm and its distance from the opposite side is 16 cm. Find the area of the parallelogram.
The base of a parallelogram is thrice it height. If its area is 768 cm2, find the base and the height of the parallelogram.
The adjacent sides of a parallelogram are 15 cm and 10 cm. If the distance between the longer sides is 6 cm, find the distance between the shorter sides.
Find the area of a triangle whose base is 30 cm and the height is 18 cm.
Find the area of a right-angled triangle whose hypotenuse is 13 cm long and one of its legs is 12 cm long.
The sides of a triangle are in the ratio 15 : 13 : 14 and its perimeter is 168 cm. Find the area of the triangle.
The diameter of the wheel of a car is 70 cm. How many revolutions will it make to travel one kilometer?
A wire is along the boundary of a circle with a radius of 28 cm. If the same wire is bent in the form of a square, find the area of the square formed.
