Advertisements
Advertisements
प्रश्न
The ratio between the areas of two circles is 16 : 9. Find the ratio between their :
(i) radius
(ii) diameters
(iii) circumference
उत्तर
(i) Let radius of first circle = r1
and radius of second circle = r2
Given that ratio of the areas of circles = 16 : 9
⇒ `(π"r"_1^2)/(π"r"_2^2)=16/9`
⇒ `(π"r"_1^2)/(π"r"_2^2)=4^2/3^2`
⇒ `("r"_1)/("r"_2)=4/3`
(ii) Let the diameter of first circle = d1
and diameter of second circle = d2
Since, we know that diameter = 2 × radius
∴ d1 = 2 × r1 = 2 × 4x = 8x
and d2 = 2 × r2 = 2 × 3x = 6x
Now, the ratio between the diameter of two circles = d1 : d2
= 8x : 6x = 4 : 3
(iii) Now, consider the ratio of circumference of the circles
= `(2π"r"_1)/(2π"r"_2)="r"_1/"r"_2=4/3`
∴ The ratio between the circumference of two circles = 4 : 3
APPEARS IN
संबंधित प्रश्न
In the figure given below, find the area of shaded region: (All measurements are in cm)
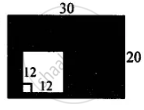
In the figure given below, find the area of shaded region: (All measurements are in cm)
Find the area of the rhombus, if its diagonals are 30 cm and 24 cm.
If the area of a rhombus is 112 cm2 and one of its diagonals is 14 cm, find its other diagonal.
Find the area of a right-angled triangle whose hypotenuse is 13 cm long and one of its legs is 12 cm long.
The sides of a triangle are 21 cm, 17 cm, and 10 cm. Find its area.
Find the area of an isosceles triangle whose base is 16 cm and the length of each of the equal sides is 10 cm.
The legs of a right-angled triangle are in the ratio 4 : 3 and its area is 4056 cm2. Find the length of its legs.
The diameter of a circle is 20 cm. Taking π = 3.14, find the circumference and its area.
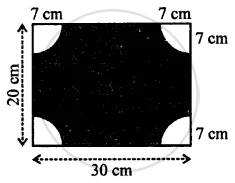
From each corner of a rectangular paper (30 cm x 20 cm) a quadrant of a circle of radius 7 cm is cut. Find the area of the remaining paper i.e., shaded portion.