Advertisements
Advertisements
प्रश्न
The equations of the lines joining the vertex of the parabola y2 = 6x to the points on it which have abscissa 24 are ______.
पर्याय
y ± 2x = 0
2y ± x = 0
x ± 2y = 0
2x ± y = 0
उत्तर
The equations of the lines joining the vertex of the parabola y2 = 6x to the points on it which have abscissa 24 are 2y ± x = 0.
Explanation: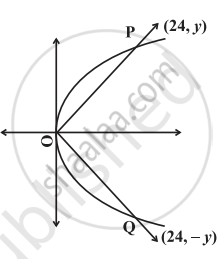
Let P and Q be points on the parabola y2 = 6x and OP
OQ be the lines joining the vertex O to the points P
And Q whose abscissa are 24.
Thus y2 = 6 × 24 = 144
or y = ± 12.
Therefore the coordinates of the points P and Q are (24, 12) and (24, –12) respectively.
Hence the lines are y = `+- 12/24 x 2y x`.
APPEARS IN
संबंधित प्रश्न
Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum.
x2 = 6y
Find the equation of the parabola that satisfies the following condition:
Focus (6, 0); directrix x = –6
Find the equation of the parabola that satisfies the following condition:
Vertex (0, 0); focus (3, 0)
Find the equation of the parabola that satisfies the following condition:
Vertex (0, 0) focus (–2, 0)
Find the equation of the parabola that satisfies the following condition:
Vertex (0, 0) passing through (2, 3) and axis is along x-axis
Find the equation of the parabola that satisfies the following condition:
Vertex (0, 0), passing through (5, 2) and symmetric with respect to y-axis.
An arch is in the form of a parabola with its axis vertical. The arch is 10 m high and 5 m wide at the base. How wide is it 2 m from the vertex of the parabola?
Find the equation of the parabola whose:
focus is (1, 1) and the directrix is x + y + 1 = 0
Find the equation of the parabola if
the focus is at (−6, −6) and the vertex is at (−2, 2)
Find the equation of the parabola if the focus is at (0, −3) and the vertex is at (−1, −3)
Find the equation of the parabola if the focus is at (a, 0) and the vertex is at (a', 0)
At what point of the parabola x2 = 9y is the abscissa three times that of ordinate?
Find the equation of a parabola with vertex at the origin and the directrix, y = 2.
Find the equations of the lines joining the vertex of the parabola y2 = 6x to the point on it which have abscissa 24.
Find the coordinates of points on the parabola y2 = 8x whose focal distance is 4.
PSQ is a focal chord of the parabola y2 = 8x. If SP = 6, then write SQ.
Write the equation of the parabola whose vertex is at (−3,0) and the directrix is x + 5 = 0.
The equation of the parabola whose vertex is (a, 0) and the directrix has the equation x + y = 3a, is
The parametric equations of a parabola are x = t2 + 1, y = 2t + 1. The cartesian equation of its directrix is
If the coordinates of the vertex and the focus of a parabola are (−1, 1) and (2, 3) respectively, then the equation of its directrix is
The locus of the points of trisection of the double ordinates of a parabola is a
The equation of the directrix of the parabola whose vertex and focus are (1, 4) and (2, 6) respectively is
If V and S are respectively the vertex and focus of the parabola y2 + 6y + 2x + 5 = 0, then SV =
The equation of the parabola whose focus is the point (2, 3) and directrix is the line x – 4y + 3 = 0 is ______.
If the line y = mx + 1 is tangent to the parabola y2 = 4x then find the value of m.
If the vertex of the parabola is the point (–3, 0) and the directrix is the line x + 5 = 0, then its equation is ______.
