Advertisements
Advertisements
प्रश्न
The equations of the lines joining the vertex of the parabola y2 = 6x to the points on it which have abscissa 24 are ______.
विकल्प
y ± 2x = 0
2y ± x = 0
x ± 2y = 0
2x ± y = 0
उत्तर
The equations of the lines joining the vertex of the parabola y2 = 6x to the points on it which have abscissa 24 are 2y ± x = 0.
Explanation: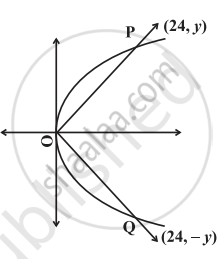
Let P and Q be points on the parabola y2 = 6x and OP
OQ be the lines joining the vertex O to the points P
And Q whose abscissa are 24.
Thus y2 = 6 × 24 = 144
or y = ± 12.
Therefore the coordinates of the points P and Q are (24, 12) and (24, –12) respectively.
Hence the lines are y = `+- 12/24 x 2y x`.
APPEARS IN
संबंधित प्रश्न
Find the equation of the parabola that satisfies the following condition:
Focus (0, –3); directrix y = 3
Find the equation of the parabola that satisfies the following condition:
Vertex (0, 0) focus (–2, 0)
Find the equation of the parabola that satisfies the following condition:
Vertex (0, 0), passing through (5, 2) and symmetric with respect to y-axis.
Find the equation of the parabola whose:
focus is (3, 0) and the directrix is 3x + 4y = 1
Find the equation of the parabola whose:
focus is (1, 1) and the directrix is x + y + 1 = 0
Find the equation of the parabola whose:
focus is (0, 0) and the directrix 2x − y − 1 = 0
Find the equation of the parabola whose:
focus is (2, 3) and the directrix x − 4y + 3 = 0.
Find the equation of the parabola if the focus is at (a, 0) and the vertex is at (a', 0)
At what point of the parabola x2 = 9y is the abscissa three times that of ordinate?
Find the equation of a parabola with vertex at the origin and the directrix, y = 2.
Find the equations of the lines joining the vertex of the parabola y2 = 6x to the point on it which have abscissa 24.
Find the coordinates of points on the parabola y2 = 8x whose focal distance is 4.
The parametric equations of a parabola are x = t2 + 1, y = 2t + 1. The cartesian equation of its directrix is
The equation 16x2 + y2 + 8xy − 74x − 78y + 212 = 0 represents
The locus of the points of trisection of the double ordinates of a parabola is a
The equation of the directrix of the parabola whose vertex and focus are (1, 4) and (2, 6) respectively is
If V and S are respectively the vertex and focus of the parabola y2 + 6y + 2x + 5 = 0, then SV =
The equation of the parabola whose focus is (1, −1) and the directrix is x + y + 7 = 0 is
The equation of the parabola whose focus is the point (2, 3) and directrix is the line x – 4y + 3 = 0 is ______.
Find the coordinates of a point on the parabola y2 = 8x whose focal distance is 4.
Find the equation of the following parabolas:
Vertex at (0, 4), focus at (0, 2)
Find the equation of the following parabolas:
Focus at (–1, –2), directrix x – 2y + 3 = 0
Find the equation of the set of all points the sum of whose distances from the points (3, 0) and (9, 0) is 12.
The equation of the parabola having focus at (–1, –2) and the directrix x – 2y + 3 = 0 is ______.
