Advertisements
Advertisements
प्रश्न
The following figure shows a conductor of length l with a circular cross-section. The radius of the cross-section varies linearly from a to b. The resistivity of the material is ρ. Assuming that b – a << l, find the resistance of the conductor.

उत्तर
Let us consider a small element strip of length dx at a distance x from one end, as shown below.
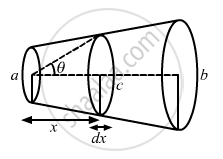
Let the resistance of the small element strip be dR. Let the radius at that point be c .
Then, the resistance of this small strip,
\[dR = \frac{\rho dx}{\pi c^2} .............(1)\]
\[\tan\theta = \frac{c - a}{x} = \frac{b - a}{L}\]
\[ \Rightarrow \frac{c - a}{x} = \frac{b - a}{L}\]
\[ \Rightarrow L \times \left( c - a \right) = x \times \left( b - a \right)\]
\[ \Rightarrow Lc - La = xb - xa\]
Differentiating w.r.t to x, we get:-
\[L\frac{dc}{dx} - 0 = b - a \]
\[ dx = \frac{Ldc}{\left( b - a \right)} ...........(2)\]
Substituting the value of dx in equation (1), we get:-
\[dR = \frac{\rho Ldc}{\pi c^2 \left( b - a \right)}\]
\[dR = \frac{\rho L}{\pi\left( b - a \right)} \cdot \frac{dc}{c^2}\]
Integrating dR from a to b, we get:-
\[\int_0^R dR = \frac{\rho L}{\pi\left( b - a \right)} \int_a^b \frac{dc}{c^2}\]
\[ \Rightarrow R = \frac{\rho L}{\pi\left( b - a \right)} \left[ \frac{- 1}{c} \right]_a^b \]
\[ = \frac{\rho L}{\pi\left( b - a \right)}\left( \frac{- 1}{b} - \frac{- 1}{a} \right)\]
\[ = \frac{\rho L}{\pi ab}\]
APPEARS IN
संबंधित प्रश्न
Define current density. Write an expression which connects current density with drift speed
Define the term 'electrical conductivity' of a metallic wire. Write its S.I. unit.
The heat developed in a system is proportional to the current through it.
An electrolysis experiment is stopped and the battery terminals are reversed.
A heater coil is to be constructed with a nichrome wire (ρ = 1.0 × 10−6 Ωm) that can operate at 500 W when connected to a 250 V supply. (a) What would be the resistance of the coil? (b) If the cross-sectional area of the wire is 0.5 mm2, what length of the wire will be needed? (c) If the radius of each turn is 4.0 mm, how many turns will be there in the coil?
For a metallic conductor, what is the relation between current density (J), conductivity (σ) and electric field intensity (E)?
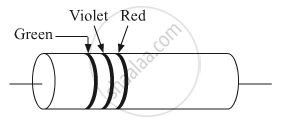
What is the colour code of a carbon resistor having a resistance of 470 Ω and a tolerance of 5%?
A carbon resistor is shown in the figure. Using color code, write the value of the resistance.
Consider a current carrying wire (current I) in the shape of a circle.
Assertion: Bending a wire does not effect electrical resistance.
Reason: Resistance of wire is proportional to resistivity of material.
The electric resistance of a certain wire of iron is R. If its length and radius are both doubled, then ______.
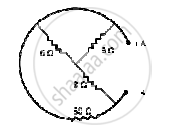
The equivalent resistance between A and B is ____________.
As the temperature of conductor increase, it's resistivity and conductivity change. The ratio of resistivity to conductivity.
The resistivity of a wire ______
Consider four conducting materials copper, tungsten, mercury and aluminium with resistivity ρC, ρT, ρM and ρA respectively. Then:
