Advertisements
Advertisements
प्रश्न
The mean of the following distribution is 62.8 and the sum of all the frequencies is 50. Find the missing frequencies f1 and f2.
| Class | 0 – 20 | 20 – 40 | 40 – 60 | 60 – 80 | 80 – 100 | 100 – 120 |
| Frequency | 5 | f1 | 10 | f2 | 7 | 8 |
उत्तर
| Class | Freq (f) | Mid value | fx |
| 0 – 20 | 5 | 10 | 50 |
| 20 – 40 | f1 | 30 | 30f1 |
| 40 – 60 | 10 | 50 | 500 |
| 60 – 80 | f2 | 70 | 70f2 |
| 80 – 100 | 7 | 90 | 630 |
| 100 – 120 | 8 | 110 | 880 |
| Total | 30 + f1 + f2 | 2060 + 30f1 + 70f2 |
Now, ∑f = 30 + f1 + f2 and ∑fx = 2060 + 30f1 + 70f2 ...(i)
∑f = 50; mean = 62.8 ...(ii)
From (i)
30 + f1 + f2 = 50
f1 + f2 = 20 ...(iii)
Using (i) and (ii)
Mean = `(2060 + 30f_1 + 70f_2)/50`
`62.8 = (2060 + 30f_1 + 70f_2)/50`
2060 + 30f1 + 70f2 = 62.8 × 50
2060 + 30f1 + 70f2 = 3140
30f1 + 70f2 = 1080
3f1 + 7f2 = 108 ...(iv)
From (iii) and (iv)
f1 = 8
f2 = 12
APPEARS IN
संबंधित प्रश्न
The median is always one of the numbers in a data.
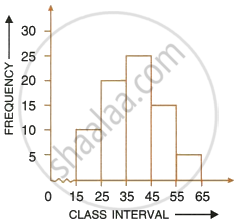
Using the information given in the adjoining histogram, calculate the mean.
If the mean of 8 , 14 , 20 , x and 12 is 13, find x.
Find the mean of the following frequency distribution :
| Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 |
| Frequency | 4 | 4 | 7 | 10 | 12 | 8 | 5 |
The mean of a certain number of observations is 32. Find the resulting mean, if the observation is, increased by 3
Find the mean of: first five odd natural numbers
If the mean of x, x + 2, x + 4, x + 6 and x + 8 is 13, find the value of x. Sum of data.
Find the median of 17, 23, 36, 12, 18, 23, 40 and 20
3, 8, 10, x, 14, 16, 18, 20 are in the ascending order and their median is 13. Calculate the numerical value of x.
Median of the data may or may not be from the given data.
