Advertisements
Advertisements
प्रश्न
Using the information given in the adjoining histogram, calculate the mean.
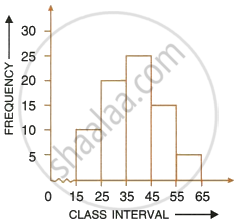
उत्तर
| C.I. | Frequency | Mid value x | fx |
| 15 – 25 | 10 | 20 | 200 |
| 25 – 35 | 20 | 30 | 600 |
| 35 – 45 | 25 | 40 | 1000 |
| 45 – 55 | 15 | 50 | 750 |
| 55 – 65 | 5 | 60 | 300 |
| Total | 75 | 2850 |
`barx = (sumf_x)/(sumf)`
= `2850/75`
= 38
APPEARS IN
संबंधित प्रश्न
The following distribution represents the height of 160 students of a school.
| Height (in cm) | No. of Students |
| 140 – 145 | 12 |
| 145 – 150 | 20 |
| 150 – 155 | 30 |
| 155 – 160 | 38 |
| 160 – 165 | 24 |
| 165 – 170 | 16 |
| 170 – 175 | 12 |
| 175 – 180 | 8 |
Draw an ogive for the given distribution taking 2 cm = 5 cm of height on one axis and 2 cm = 20 students on the other axis. Using the graph, determine:
- The median height.
- The interquartile range.
- The number of students whose height is above 172 cm.
Marks obtained (in mathematics) by 9 student are given below:
60, 67, 52, 76, 50, 51, 74, 45 and 56
if marks of each student be increased by 4; what will be the new value of arithmetic mean.
By drawing an ogive, estimate the median for the following frequency distribution:
| Weight (kg) | 10 – 15 | 15 – 20 | 20 – 25 | 25 – 30 | 30 – 35 |
| No. of boys | 11 | 25 | 12 | 5 | 2 |
The marks of 20 students in a test were as follows:
2, 6, 8, 9, 10, 11, 11, 12, 13, 13, 14, 14, 15, 15, 15, 16, 16, 18, 19 and 20.
Calculate:
- the mean
- the median
- the mode
The distribution, given below, shows the marks obtained by 25 students in an aptitude test. Find the mean, median and mode of the distribution.
| Marks obtained | 5 | 6 | 7 | 8 | 9 | 10 |
| No. of students | 3 | 9 | 6 | 4 | 2 | 1 |
Find the mode of the following frequency distribution:
| Hrs. Spent daily in studies | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 | 6.5 |
| No. of students | 8 | 7 | 3 | 5 | 10 | 6 | 3 | 4 |
In 10 numbers, arranged in increasing order, the 7th number is increased by 8, how much will the median be changed?
Find the mean of: 7, 5, 0, 3, 0, 6, 0, 9, 1 and 4
Find the mean of: first five odd natural numbers
The mean of five positive integers is twice their median. If four of the integers are 3, 4, 6, 9 and median is 6, then find the fifth integer
