Advertisements
Advertisements
प्रश्न
The pathway of a square paddy field has 5 m width and length of its side is 40 m. Find the total area of its pathway. (Note: Use suitable identity)
Advertisements
उत्तर
Given side of the square = 40 m
Also width of the pathway = 5 m
∴ Side of the larger square = 40 m + 2(5) m
= 40 m + 10 m
= 50 m
Area of the pathway = area of large square – area of smaller square
= 502 – 402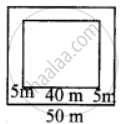 
Substituting a = 50 and b = 40 in
a2 – b2 = (a + b)(a – b) we have
502 – 402 = (50 + 40)(50 – 40)
Area of pathway = 90 × 10
Area of the pathway = 900 m2
APPEARS IN
संबंधित प्रश्न
Factorise the following algebraic expression by using the identity a2 – b2 = (a + b)(a – b)
z2 – 16
If X = a2 – 1 and Y = 1 – b2, then find X + Y and factorize the same
Using suitable identities, evaluate the following.
(339)2 – (161)2
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
p5 – 16p
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
x4 – y4
The sum of (x + 5) observations is x4 – 625. Find the mean of the observations.
The base of a parallelogram is (2x + 3 units) and the corresponding height is (2x – 3 units). Find the area of the parallelogram in terms of x. What will be the area of parallelogram of x = 30 units?
Verify the following:
(m + n)(m2 – mn + n2) = m3 + n3
Verify the following:
`((3p)/7 + 7/(6p))^2 - (3/7p + 7/(6p))^2 = 2`
The product of two expressions is x5 + x3 + x. If one of them is x2 + x + 1, find the other.
