Advertisements
Advertisements
प्रश्न
The ratio of masses of two planets is 2:3 and the ratio of their radii is 4:7 Find the ratio of their accelerations due to gravity.
उत्तर
The ratio of masses of two planets m1: m2 = 2 : 3
The ratio of radii of two planets R1: R2 = 4: 7
Formula:
g= `"GM"/R^2` ∴ g ∝ `"M"/"R"^2`
`"g"_1/"g"_2` = `"M"_1/"M"_2` . `"R"_2^2/"R"_1^2` = `2/3xx 7^2/4^2` = `(2xx49)/(3xx16)` = `98/48`
`"g"_1/"g"_2` = `49/24`
APPEARS IN
संबंधित प्रश्न
State whether the following statement is true or false :
The value of G on the moon is about one-sixth `(1/6)`of the value of G on the earth.
Is the acceleration due to gravity of earth ‘g’ a constant ? Discuss.
Write scientific reason.
The weight of an object varies on different planets.
______ is used to change the speed of the car.
The depth 'd' below the surface of the earth at which acceleration due to gravity becomes `(g/n)` is ______.
R = radius of the earth, 'g' = acceleration due to gravity, n = integer
A wire AB is carrying steady current 'I1' and is kept on the table. Another wire CD carrying current 'I2' is held parallel and directly above AB at a distance 'r'. When wire CD is left free and it remains suspended at its position, its mass per unit length is (g =acceleration due to gravity) ____________.
Suppose the gravity of the earth suddenly becomes zero, then in which direction will the moon begin to move if no other celestial body affects it?
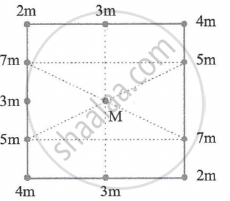
A central particle M is surrounded by a square array of other particles, separated by either distanced or distance d/2 along the perimeter o the square. The magnitude of the gravitational force on the central particle due to the other particles is ______.
The moon has a mass of 1/81 that of the earth and a radius of 1/4 that of the earth. The escape speed from the surface of the earth is 11.2 km/s. The escape speed from the surface of the moon is ______.
The difference in the acceleration due to gravity at the pole and equator is ______.
(g = acceleration due to gravity, R = radius of the earth; θ = latitude, ω = angular velocity, cos0° = 1, cos90° = 0)
