Advertisements
Advertisements
प्रश्न
The sales of a commodity in tones varied from January 2010 to December 2010 as follows:
| In Year 2010 | Sales (in tones) |
| Jan | 280 |
| Feb | 240 |
| Mar | 270 |
| Apr | 300 |
| May | 280 |
| Jun | 290 |
| Jul | 210 |
| Aug | 200 |
| Sep | 230 |
| Oct | 200 |
| Nov | 230 |
| Dec | 210 |
Fit a trend line by the method of semi-average
उत्तर
Since the number of months is even (12), we can equally divide the given data into two equal parts and obtain the averages of the first six months and last six months
| In Year 2010 |
Sales (in tones) |
Average |
| Jan | 280 | `(280 + 240 + 270 + 300 + 280 + 290)/6` = 276.667 |
| Feb | 240 | |
| Mar | 270 | |
| Apr | 300 | |
| May | 280 | |
| Jun | 290 | |
| Jul | 210 | `(210 + 200 + 230 + 200 + 230 + 210)/6` = 213.33 |
| Aug | 200 | |
| Sep | 230 | |
| Oct | 200 | |
| Nov | 230 | |
| Dec | 210 |
Thus we obtain semi-average I = 276.667 and semi-average II = 213.333
To fit a trend line we plot each value at the mid-point (month) of each half.
i.e we plot 276.667 in the middle of March and April
we plot 213.333 in the middle of September and October.
We join the two points by a straight line.
This is the required line.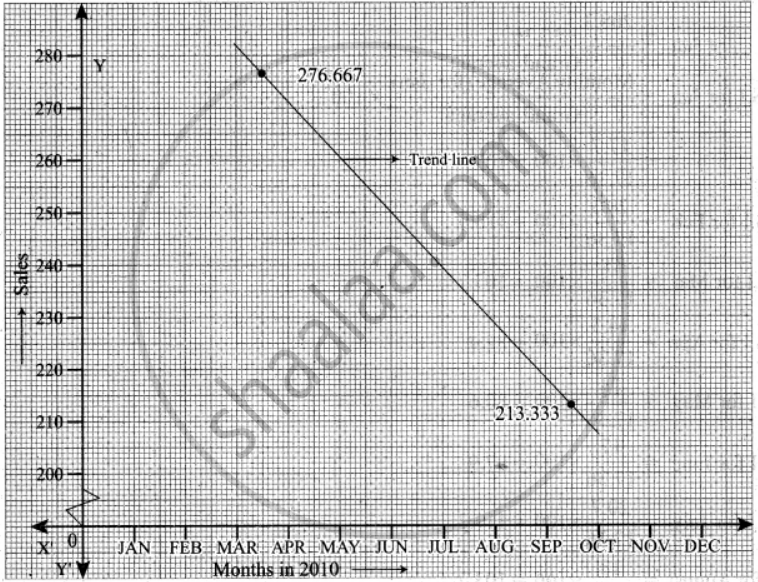
APPEARS IN
संबंधित प्रश्न
What is the need for studying time series?
Explain cyclic variations
Discuss about irregular variation
State the different methods of measuring trend
Compute the average seasonal movement for the following series
| Year | Quarterly Production | |||
| I | II | III | IV | |
| 2002 | 3.5 | 3.8 | 3.7 | 3.5 |
| 2203 | 3.6 | 4.2 | 3. | 4.1 |
| 2004 | 3.4 | 3.9 | 37 | 4.2 |
| 2005 | 4.2 | 4.5 | 3 | 4.4 |
| 2006 | 3.9 | 4.4 | 4.2 | 4.6 |
Use the method of monthly averages to find the monthly indices for the following data of production of a commodity for the years 2002, 2003 and 2004
| 2002 | 2003 | 2004 |
| 15 | 20 | 18 |
| 18 | 18 | 25 |
| 17 | 16 | 21 |
| 19 | 13 | 11 |
| 16 | 12 | 14 |
| 20 | 15 | 16 |
| 21 | 22 | 19 |
| 18 | 16 | 20 |
| 17 | 18 | 1 |
| 15 | 20 | 16 |
| 14 | 17 | 18 |
| 18 | 15 | 20 |
The following table shows the number of salesmen working for a certain concern:
| Year | 1992 | 1993 | 1994 | 1995 | 1996 |
| No. of salesman |
46 | 48 | 42 | 56 | 52 |
Use the method of least squares to fit a straight line and estimate the number of salesmen in 1997
Choose the correct alternative:
The additive model of the time series with the components T, S, C and I is
Choose the correct alternative:
The component of a time series attached to long term variation is trended as
The sum of the infinite series `x + (1 + 2)/(2!) x^2 + (1 + 2 + 3)/(3!) x^3 +` .... equals
