Question

The vertices of a triangle are A (1, 4), B (2, 3) and C (1, 6). Find equations of altitudes of ΔABC

Answer 1

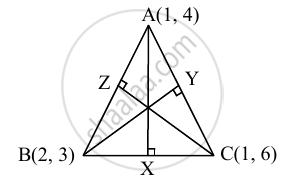
Let AX, BY and CZ be the altitudes through the vertices A, B and C respectively of ΔABC.
Slope of BC = – 3

∴ slope of AX = `1/3`       ...[∵ AX ⊥ BC]
Since, altitude AX passes through (1, 4) and has slope `1/3`
∴ equation of altitude AX is

y – 4 = `1/3(x - 1)`

∴ 3y – 12 = x – 1
∴ x – 3y + 11 = 0
Since, both the points A and C have same x co-ordinates i.e. 1
∴ the points A and C lie on the line x = 1.
AC is parallel to Y-axis and therefore, altitude
BY is parallel to X-axis.
Since, the altitude BY passes through B(2, 3).
∴ the equation of altitude BY is y = 3.
Also, slope of AB = – 1
∴ slope of CZ = 1       ...[∵ CZ ⊥ AB]
Since, altitude CZ passes through (1, 6) and has slope 1
∴ equation of altitude CZ is
∴ y – 6 = 1(x – 1)
∴ x – y + 5 = 0.