Advertisements
Advertisements
प्रश्न
Find the equation of the line: through the origin which bisects the portion of the line 3x + 2y = 2 intercepted between the co-ordinate axes.
उत्तर
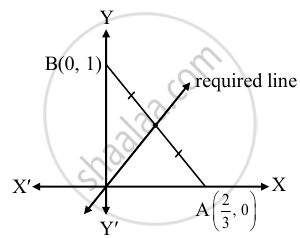
Given equation of the line is 3x + 2y = 2.
∴ `(3x)/2 + (2y)/2` = 1
∴ `x/(2/3) + y/1` = 1
This equation is of the form `x/"a" + y/"b" ` = 1, with a = `2/3`, b = 1.
∴ the line 3x + 2y = 2 intersects the X-axis at `"A"(2/3, 0)` and Y-axis at B(0, 1).
Required line is passing through the midpoint of AB.
∴ Midpoint of AB = `((2/3 + 0)/2, (0 + 1)/2) = (1/3, 1/2)`
∴ Required line passes through (0, 0) and `(1/3, 1/2)`.
Equation of the line in two point form is
`(y - y_1)/(y_2 - y_1) = (x - x_1)/(x_2 - x_1)`
∴ the equation of the required line is
`(y - 0)/(1/2 - 0) = (x - 0)/(1/3 - 0)`
∴ 2y = 3x
∴ 3x –2y = 0
APPEARS IN
संबंधित प्रश्न
Find the equation of the line passing through the points A(2, 0) and B(3, 4).
Line y = mx + c passes through the points A(2, 1) and B(3, 2). Determine m and c.
The vertices of a triangle are A(3, 4), B(2, 0) and C(1, 6). Find the equation of the median AD.
Find the x and y-intercepts of the following line: `x/3 + y/2` = 1
Find the equations of a line containing the point A(3, 4) and making equal intercepts on the co-ordinate axes.
Find the slope, x-intercept, y-intercept of the following line : 2x + 3y – 6 = 0
Write the following equation in ax + by + c = 0 form: y = 2x – 4
Write the following equation in ax + by + c = 0 form: `x/3 = y/2`
Reduce the equation 6x + 3y + 8 = 0 into slope-intercept form. Hence, find its slope.
Verify that A(2, 7) is not a point on the line x + 2y + 2 = 0.
Find the X-intercept of the line x + 2y – 1 = 0
Find the equation of the line: having slope 5 and containing point A(– 1, 2).
Find the equation of the line: containing the point (2, 1) and having slope 13.
The vertices of a triangle are A (1, 4), B (2, 3) and C (1, 6). Find equations of the sides
The vertices of a triangle are A (1, 4), B (2, 3) and C (1, 6). Find equations of the medians
