Question

Find the equation of the line: through the origin which bisects the portion of the line 3x + 2y = 2 intercepted between the co-ordinate axes.

Answer 1

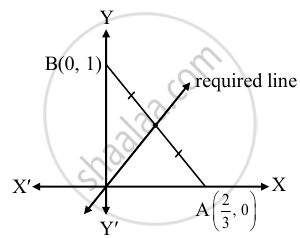
Given equation of the line is 3x + 2y = 2.

∴ `(3x)/2 + (2y)/2` = 1

∴ `x/(2/3) + y/1` = 1

This equation is of the form `x/"a" + y/"b" ` = 1, with a = `2/3`, b = 1.

∴ the line 3x + 2y = 2 intersects the X-axis at `"A"(2/3, 0)` and Y-axis at B(0, 1).

Required line is passing through the midpoint of AB.

∴ Midpoint of AB = `((2/3 + 0)/2, (0 + 1)/2) = (1/3, 1/2)`

∴ Required line passes through (0, 0) and `(1/3, 1/2)`.

Equation of the line in two point form is

`(y - y_1)/(y_2 - y_1) = (x - x_1)/(x_2 - x_1)`

∴ the equation of the required line is

`(y - 0)/(1/2 - 0) = (x - 0)/(1/3 - 0)`

∴ 2y = 3x
∴ 3x –2y = 0