Question

The vertices of a triangle are A (1, 4), B (2, 3) and C (1, 6). Find equations of the medians

Answer 1

Vertices of ΔABC are A(1, 4), B(2, 3) and C(1, 6)
Let D, E and F be the midpoints of sides BC,
AC and AB respectively of ΔABC.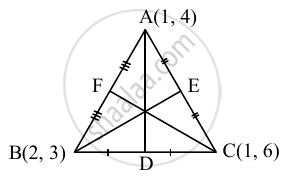

Then D = `((2 + 1)/2, (3 + 6)/2) = (3/2, 9/2)`

E = `((1 + 1)/2, (6 + 4)/2)` = (1 , 5)

F = `(( 1 + 2)/2, (4 + 3)/2) = (3/2, 7/2)` 

Equation of median AD is

`(y - 4)/(9/2 - 4) = (x - 1)/(3/2 - 1)`

∴ `(y  - 4)/(1/2) = (x - 1)/(1/2)`

∴ y – 4 = x – 1
∴ x – y + 3 = 0
Equation of median BE is

`(y - 3)/(5 - 3) = (x - 2)/(1 - 2)`

∴ `(y - 3)/2 = (x - 2)/(- 1)`

∴ – 1(y - 3) = 2(x – 2)
∴  – y + 3 = 2x –– 4
∴  2x + y = 7
Equation of median CF is

`(y - 6)/(7/2 - 6) = (x - 1)/(3/2 - 1)`

∴ `(y - 6)/(-5/2) = (x - 1)/(1/2)`

∴ `(y - 6)/(-5) = (x - 1)/1`

∴ y – 6 = – 5(x – 1)
∴ y – 6 = – 5 + 5
∴ 5x + y – 11 = 0