Advertisements
Advertisements
प्रश्न
Three identical coins, each of diameter 6 cm are placed as shown. Find the area of the shaded region between the coins. (π = 3.14) `(sqrt(3) = 1.732)`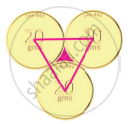
उत्तर
Given diameter of the coins = 6 cm
∴ Radius of the coins = `6/2` = 3 cm
Area of the shaded region = Area of equilateral triangle – Area of 3 sectors of angle 60°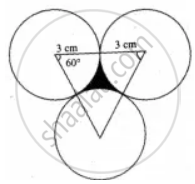
Area of the equilateral triangle = `sqrt(3)/4 "a"^2 "units"^2`
= `sqrt(3)/4 xx 6 xx 6 "cm"^2`
= `(1.732)/4 xx 6 xx 6 "m"^2`
= 15.588 cm2
Area of 3 sectors = `3 xx theta/(360^circ) xx pi"r"^2 "sq.units"`
= `3 xx (60^circ)/(360^circ) xx 3.14 xx 3 xx 3 "cm"^2`
= 1.458 cm2
∴ Area of the shaded region = 15.588 – 14.13 cm2
= 1.458 cm2
Required area = 1.458 cm2 ...(approximately)
APPEARS IN
संबंधित प्रश्न
From the measures given below, find the area of the sectors.
Length of the arc = 48 m, r = 10 m
From the measures given below, find the area of the sector.
length of the arc = 50 cm, r = 13.5 cm
A circle of radius 70 cm is divided into 5 equal sectors. Find the area of each of the sectors
Dhamu fixes a square tile of 30 cm on the floor. The tile has a sector design on it as shown in the figure. Find the area of the sector. (π = 3.14)
A circle is formed with 8 equal granite stones as shown in the figure each of radius 56 cm and whose central angle is 45°. Find the area of the granite stones. `(pi = 22/7)`
Guna has fixed a single door of width 3 feet in his room where as Nathan has fixed a double door, each of width `1 1/2` feet in his room. From the closed position, if each of the single and double doors can open up to 120°, whose door takes a minimum area?
In a rectangular field which measures 15 m × 8m, cows are tied with a rope of length 3 m at four corners of the field and also at the centre. Find the area of the field where none of the cow can graze. (π = 3.14)
