Advertisements
Advertisements
प्रश्न
Three of the six vertices of a regular hexagon are chosen at random. What is the probability that the triangle with these vertices is equilateral?
पर्याय
`3/10`
`3/20`
`1/20`
`1/10`
उत्तर
`1/10`
Explanation: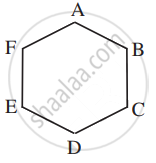
ABCDEF is a regular hexagon.
Total number of triangles 6C3 = 20. ....(Since no three points are collinear).
Of these only ∆ACE; ∆BDF are equilateral triangles.
Therefore, required probability = `2/20 = 1/10`.
APPEARS IN
संबंधित प्रश्न
A die is thrown repeatedly until a six comes up. What is the sample space for this experiment?
If a coin is tossed three times (or three coins are tossed together), then describe the sample space for this experiment.
Write the sample space for the experiment of tossing a coin four times.
What is the total number of elementary events associated to the random experiment of throwing three dice together?
An experiment consists of tossing a coin and then tossing it second time if head occurs. If a tail occurs on the first toss, then a die is tossed once. Find the sample space.
A coin is tossed twice. If the second draw results in a head, a die is rolled. Write the sample space for this experiment.
A bag contains 4 identical red balls and 3 identical black balls. The experiment consists of drawing one ball, then putting it into the bag and again drawing a ball. What are the possible outcomes of the experiment?
In a random sampling three items are selected from a lot. Each item is tested and classified as defective (D) or non-defective (N). Write the sample space of this experiment.
A bag contains one white and one red ball. A ball is drawn from the bag. If the ball drawn is white it is replaced in the bag and again a ball is drawn. Otherwise, a die is tossed. Write the sample space for this experiment.
A box contains 1 white and 3 identical black balls. Two balls are drawn at random in succession without replacement. Write the sample space for this experiment.
A die is thrown repeatedly until a six comes up. What is the sample space for this experiment.
A coin is tossed. Find the total number of elementary events and also the total number events associated with the random experiment.
A card is drawn at random from a pack of 52 cards. Find the probability that the card drawn is a black king
A card is drawn at random from a pack of 52 cards. Find the probability that the card drawn is either a black card or a king
A bag contains 6 red, 4 white and 8 blue balls. If three balls are drawn at random, find the probability that two are blue and one is red
Five cards are drawn from a pack of 52 cards. What is the chance that these 5 will contain at least one ace?
The letters of the word' CLIFTON' are placed at random in a row. What is the chance that two vowels come together?
20 cards are numbered from 1 to 20. One card is drawn at random. What is the probability that the number on the cards is not a multiple of 4?
20 cards are numbered from 1 to 20. One card is drawn at random. What is the probability that the number on the cards is odd?
20 cards are numbered from 1 to 20. One card is drawn at random. What is the probability that the number on the cards is divisible by 5?
A class consists of 10 boys and 8 girls. Three students are selected at random. What is the probability that the selected group has at least one girl?
Five cards are drawn from a well-shuffled pack of 52 cards. Find the probability that all the five cards are hearts.
An urn contains 7 white, 5 black and 3 red balls. Two balls are drawn at random. Find the probability that one ball is red and the other is black
An integer is chosen at random from first 200 positive integers. Find the probability that the integer is divisible by 6 or 8.
In a large metropolitan area, the probabilities are 0.87, 0.36, 0.30 that a family (randomly chosen for a sample survey) owns a colour television set, a black and white television set, or both kinds of sets. What is the probability that a family owns either any one or both kinds of sets?
A sample space consists of 9 elementary events E1, E2, E3, ..., E9 whose probabilities are
P(E1) = P(E2) = 0.08, P(E3) = P(E4) = P(E5) = 0.1, P(E6) = P(E7) = 0.2, P(E8) = P(E9) = 0.07
Suppose A = {E1, E5, E8}, B = {E2, E5, E8, E9}
Using the addition law of probability, find P(A ∪ B).
A sample space consists of 9 elementary events E1, E2, E3, ..., E9 whose probabilities are
P(E1) = P(E2) = 0.08, P(E3) = P(E4) = P(E5) = 0.1, P(E6) = P(E7) = 0.2, P(E8) = P(E9) = 0.07
Suppose A = {E1, E5, E8}, B = {E2, E5, E8, E9}
Calculate \[P\left( \bar{ B} \right)\] from P(B), also calculate \[P\left( \bar{ B } \right)\] directly from the elementary events of \[\bar{ B } \] .
Three dice are thrown simultaneously. What is the probability of getting 15 as the sum?
If E and E2 are independent evens, write the value of P \[\left( ( E_1 \cup E_2 ) \cap (E \cap E_2 ) \right)\]
An urn contains nine balls of which three are red, four are blue and two are green. Three balls are drawn at random without replacement from the urn. The probability that the three balls have different colours is ______.
