Advertisements
Advertisements
प्रश्न
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
उत्तर

It is given that AC is the tangent to the smaller circle. We know that the tangent to a circle is perpendicular to the radius through the point of contact.
∴ OB ⊥ AC
In ∆OBA,
\[\left( OB \right)^2 + \left( AB \right)^2 = \left( OA \right)^2 \left[ \text{Using Pythagoras theorem} \right]\]
\[ \Rightarrow b^2 + \left( AB \right)^2 = a^2 \]
\[ \Rightarrow \left( AB \right)^2 = a^2 - b^2 \]
\[ \Rightarrow AB = \sqrt{a^2 - b^2}\]
Since AC is the chord of the larger circle,
∴ AB = BC (Perpendicular from the centre of a circle to the chord, bisects the chord.)
∴ AC = 2AB = 2
APPEARS IN
संबंधित प्रश्न
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ∠ACB=90° and AC = 15 cm.

If the perimeter of a semi-circular protractor is 36 cm, then its diameter is
The perimeter of the sector OAB shown in the following figure, is

If diameter of a circle is increased by 40%, then its area increase by
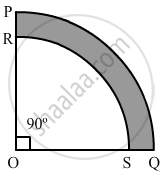
In the given figure, PQRS represents a flower bed. If OP = 21 m and OR = 14 m, find the area of the flower bed.
Find the area of a ring whose outer and inner radii are respectively 23 cm and 12 cm.
ABCD is a field in the shape of a trapezium, AD || BC, ∠ABC = 90° and ∠ADC = 60°. Four sectors are formed with centres A, B, C and D, as shown in the figure. The radius of each sector is 14 m. Find the following:
- total area of the four sectors,
- area of the remaining portion, given that AD = 55 m, BC = 45 m and AB = 30 m.

A circle of the largest area is cut from a rectangular piece of cardboard with dimensions 55 cm and 42 cm. Find the ratio between the area of the circle cut and the area of the remaining card-board.
In a grassland, a sheep is tethered by a rope of length 4.9 m. Find the maximum area that the sheep can graze
Area of a circle with diameter ‘m’ radius ‘n’ and circumference ‘p’ is ______.
