Advertisements
Advertisements
प्रश्न
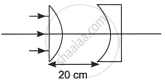
Two converging lenses of unequal focal lengths can be used to reduce the aperture of a parallel beam of light without loosing the energy of the light. This increase the intensity. Describe how the converging lenses should be placed to do this.
उत्तर
Let the two converging lenses be L1 and L2, with focal lengths f1 and f2 respectively.
To reduce the aperture of a parallel beam of light without losing the energy of the light and also increase the intensity, we have to place the lens L2 within the focal range of L1.
APPEARS IN
संबंधित प्रश्न
A beam of light converges at a point P. Now a lens is placed in the path of the convergent beam 12 cm from P. At what point does the beam converge if the lens is
- a convex lens of focal length 20 cm, and
- a concave lens of focal length 16 cm?
An object of size 3.0 cm is placed 14 cm in front of a concave lens of focal length 21 cm. Describe the image produced by the lens. What happens if the object is moved further away from the lens?
The image of a small electric bulb fixed on the wall of a room is to be obtained on the opposite wall 3 m away by means of a large convex lens. What is the maximum possible focal length of the lens required for the purpose?
A screen is placed 90 cm from an object. The image of the object on the screen is formed by a convex lens at two different locations separated by 20 cm. Determine the focal length of the lens.
A card sheet divided into squares each of size 1 mm2 is being viewed at a distance of 9 cm through a magnifying glass (a converging lens of focal length 9 cm) held close to the eye.
- What is the magnification produced by the lens? How much is the area of each square in the virtual image?
- What is the angular magnification (magnifying power) of the lens?
- Is the magnification in (a) equal to the magnifying power in (b)? Explain.
Figure shows an equiconvex lens (of refractive index 1.50) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be 45.0 cm. The liquid is removed and the experiment is repeated. The new distance is measured to be 30.0 cm. What is the refractive index of the liquid?
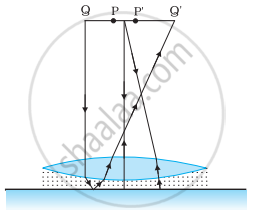
Two concave lenses L1 and L2 are kept in contact with each other. If the space between the two lenses is filled with a material of smaller refractive index, the magnitude of the focal length of the combination
A small piece of wood is floating on the surface of a 2.5 m deep lake. Where does the shadow form on the bottom when the sum is just setting? Refractive index of water = 4/3.
A pin of length 2.0 cm lies along the principal axis of a converging lens, the centre being at a distance of 11 cm from the lens. The focal length of the lens is 6 cm. Find the size of the image.
Answer the following question.
An optical instrument uses a lens of 100 D for the objective lens and 50 D for its eyepiece. When the tube length is kept at 20 cm, the final image is formed at infinity.
(a) Identify the optical instrument.
(b) Calculate the magnification produced by the instrument.
An object approaches a convergent lens from the left of the lens with a uniform speed 5 m/s and stops at the focus. The image ______.
Will the focal length of a lens for red light be more, same or less than that for blue light?
In many experimental set-ups the source and screen are fixed at a distance say D and the lens is movable. Show that there are two positions for the lens for which an image is formed on the screen. Find the distance between these points and the ratio of the image sizes for these two points.
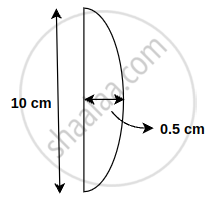
A plano convex lens has diameter of 10 cm and its thickness at the centre is 0.5 cm. Speed of light in the lens is 2 × 108 ms-1. What is the focal length of the lens?
In the given figure the radius of curvature of the curved face in the planoconvex and the planoconcave lens is 15 cm each. The refractive index of the material of the lenses is 1.5. Find the final position of the image formed.