Advertisements
Advertisements
प्रश्न
Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0 × 10−22 C/m2. What is E:
- in the outer region of the first plate,
- in the outer region of the second plate, and
- between the plates?
उत्तर
The situation is represented in the following figure.
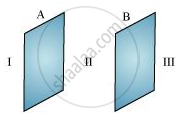
A and B are two parallel plates close to each other. Outer region of plate A is labelled as I, the outer region of plate B is labelled as III, and the region between the plates, A and B, is labelled as II.
Charge density of plate A, σ = 17.0 × 10−22 C/m2
Charge density of plate B, σ = −17.0 × 10−22 C/m2
In regions, I and III, electric field E is zero. This is because the charge is not enclosed by the respective plates.
Electric field E in region II is given by the relation,
`"E" = sigma/in_0`
Where,
∈0 = Permittivity of free space = 8.854 × 10−12 N−1 C2 m−2
∴ `"E" = (17.0 xx 10^-22)/(8.854 xx 10^-12)`
= 1.92 × 10−10 N/C
Therefore, the electric field between the plates is 1.92 × 10−10 N/C.
APPEARS IN
संबंधित प्रश्न
Use Gauss's law to find the electric field due to a uniformly charged infinite plane sheet. What is the direction of field for positive and negative charge densities?
Find the electric field intensity due to a uniformly charged spherical shell at a point (i) outside the shell. Plot the graph of electric field with distance from the centre of the shell.
Find the electric field intensity due to a uniformly charged spherical shell at a point (ii) inside the shell. Plot the graph of electric field with distance from the centre of the shell.
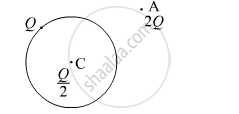
A thin metallic spherical shell of radius R carries a charge Q on its surface. A point charge`Q/2` is placed at its centre C and an other charge +2Q is placed outside the shell at a distance x from the centre as shown in the figure. Find (i) the force on the charge at the centre of shell and at the point A, (ii) the electric flux through the shell.
Find the ratio of the potential differences that must be applied across the parallel and series combination of two capacitors C1 and C2 with their capacitances in the ratio 1 : 2 so that the energy stored in the two cases becomes the same.
An infinitely large thin plane sheet has a uniform surface charge density +σ. Obtain the expression for the amount of work done in bringing a point charge q from infinity to a point, distant r, in front of the charged plane sheet.
Using Gauss’ law deduce the expression for the electric field due to a uniformly charged spherical conducting shell of radius R at a point
(i) outside and (ii) inside the shell.
Plot a graph showing variation of electric field as a function of r > R and r < R.
(r being the distance from the centre of the shell)
How is the field directed if (i) the sheet is positively charged, (ii) negatively charged?
A charge Q is uniformly distributed on a spherical shell. What is the field at the centre of the shell? If a point charge is brought close to the shell, will the field at the centre change? Does your answer depend on whether the shell is conducting or non-conducting?
A spherical shell made of plastic, contains a charge Q distributed uniformly over its surface. What is the electric field inside the shell? If the shell is hammered to deshape it, without altering the charge, will the field inside be changed? What happens if the shell is made of a metal?
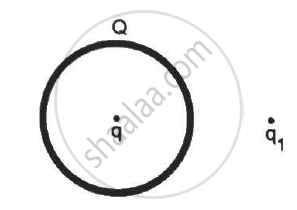
A thin, metallic spherical shell contains a charge Q on it. A point charge q is placed at the centre of the shell and another charge q1 is placed outside it as shown in the following figure . All the three charges are positive. The force on the charge at the centre is ____________.
A positive point charge Q is brought near an isolated metal cube.
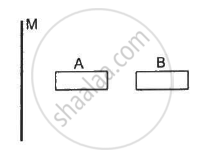
A large non-conducting sheet M is given a uniform charge density. Two uncharged small metal rods A and B are placed near the sheet as shown in the following figure.
(a) M attracts A.
(b) M attracts B.
(c) A attracts B.
(d) B attracts A.
A circular wire-loop of radius a carries a total charge Q distributed uniformly over its length. A small length dL of the wire is cut off. Find the electric field at the centre due to the remaining wire.
