Advertisements
Advertisements
प्रश्न
Using Gauss’ law deduce the expression for the electric field due to a uniformly charged spherical conducting shell of radius R at a point
(i) outside and (ii) inside the shell.
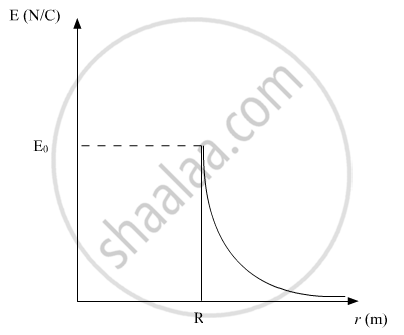
Plot a graph showing variation of electric field as a function of r > R and r < R.
(r being the distance from the centre of the shell)
उत्तर
Electric Field Due To A Uniformly Charged Thin Spherical Shell:
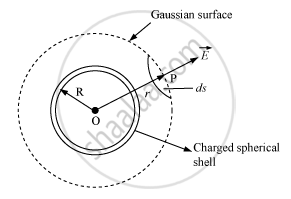
(i) When point P lies outside the spherical shell:
Suppose that we have to calculate electric field at the point P at a distance r (r > R) from its centre. Draw the Gaussian surface through point P so as to enclose the charged spherical shell. The Gaussian surface is a spherical shell of radius r and centre O.
Let `vecE`be the electric field at point P. Then, the electric flux through area element vecdsis given by,
`dphi = vecE.vecds`
Since `vecds` s also along normal to the surface,
dΦ = E ds
∴ Total electric flux through the Gaussian surface is given by,
`phi = oint_s Eds = Eoint_s ds`
Now,
`oint ds = 4pir^2`
`therefore phi= E xx 4pir^2 ..... (1)`
Since the charge enclosed by the Gaussian surface is q, according to Gauss theorem,
`phi = q/epsi_0 ......(2)`
From equations (i) and (ii), we obtain
`E xx 4pir^2q/epsi_o`
`E = 1/(4piepsi_0).q/r^2` (for r>R)
(ii) When point P lies inside the spherical shell:
In such a case, the Gaussian surface encloses no charge.
According to Gauss law,
E × 4πr2 = 0
i.e., = E = 0 (r < R)
Graph showing the variation of electric field as a function of r:
APPEARS IN
संबंधित प्रश्न
Find the electric field intensity due to a uniformly charged spherical shell at a point (ii) inside the shell. Plot the graph of electric field with distance from the centre of the shell.
A point object is placed on the principal axis of a convex spherical surface of radius of curvature R, which separates the two media of refractive indices n1 and n2 (n2 > n1). Draw the ray diagram and deduce the relation between the object distance (u), image distance (v) and the radius of curvature (R) for refraction to take place at the convex spherical surface from rarer to denser medium.
Using Gauss’s law, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the distance from it.
A spherical shell made of plastic, contains a charge Q distributed uniformly over its surface. What is the electric field inside the shell? If the shell is hammered to deshape it, without altering the charge, will the field inside be changed? What happens if the shell is made of a metal?
A rubber balloon is given a charge Q distributed uniformly over its surface. Is the field inside the balloon zero everywhere if the balloon does not have a spherical surface?
A positive point charge Q is brought near an isolated metal cube.
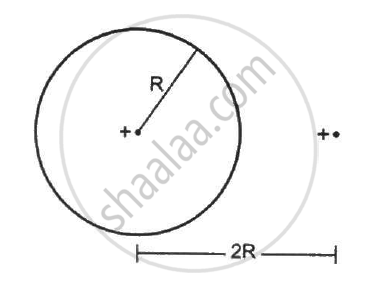
Find the flux of the electric field through a spherical surface of radius R due to a charge of 10−7 C at the centre and another equal charge at a point 2R away from the centre in the following figure.
A spherical volume contains a uniformly distributed charge of density 2.0 × 10 -4 Cm-3 Find the electric field at a point inside the volume at a distance 4⋅0 cm from the centre.
A circular wire-loop of radius a carries a total charge Q distributed uniformly over its length. A small length dL of the wire is cut off. Find the electric field at the centre due to the remaining wire.
