Advertisements
Advertisements
प्रश्न
Two long, straight wires, each carrying a current of 5 A, are placed along the x- and y-axis respectively. The currents point along the positive directions of the axes. Find the magnetic fields at the points (a) (1 m, 1 m), (b) (−1 m, 1 m), (c) (−1 m, −1 m) and (d) (1 m, −1 m).
उत्तर
Given:
Magnitude of current, I = 5 A
Separation of the point from the wire, d = 1 m
Thus, the magnitude of magnetic field due to current in the wires is given by
\[B_1 = B_2 = \frac{\mu_0 I}{2\pi d}\]
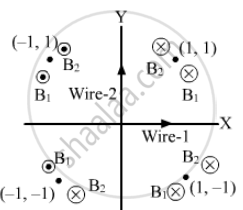
(a) At point (1 m, 1 m), the magnetic fields due to the wires are the same in magnitude, but they are opposite in direction.
Hence, the net magnetic field is zero.
(b) At point (−1 m, 1 m), the magnetic fields due to the wires are in upward direction.
\[\Rightarrow B_{net} = B_1 + B_2 \]
\[ = \left( \frac{2 \times {10}^{- 7} \times 5}{1} + \frac{2 \times {10}^{- 7} \times 5}{1} \right)\]
= 2 × 10−6 T (Along the z-axis)
(c) At point (−1 m, −1 m), the magnetic fields due to the wires are the same in magnitude, but they are opposite in direction.
Hence, the net magnetic field is zero.
(d) At point (1 m, −1 m), the magnetic fields due to the wires are in upward direction.
\[\Rightarrow B_{net} = B_1 + B_2 \]
\[ = \left( \frac{2 \times {10}^{- 7} \times 5}{1} + \frac{2 \times {10}^{- 7} \times 5}{1} \right)\]
= 2 × 10−6 T (Along the negative z-axis)
APPEARS IN
संबंधित प्रश्न
Two infinitely long straight parallel wires, '1' and '2', carrying steady currents I1 and I2 in the same direction are separated by a distance d. Obtain the expression for the magnetic field `vecB`due to the wire '1' acting on wire '2'. Hence find out, with the help of a suitable diagram, the magnitude and direction of this force per unit length on wire '2' due to wire '1'. How does the nature of this force changes if the currents are in opposite direction? Use this expression to define the S.I. unit of current.
The figure shows three infinitely long straight parallel current carrying conductors. Find the
(i) magnitude and direction of the net magnetic field at point A lying on conductor 1,
(ii) magnetic force on conductor 2.

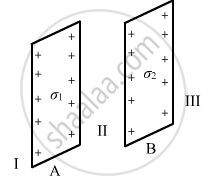
Two infinitely large plane thin parallel sheets having surface charge densities σ1 and σ2 (σ1 > σ2) are shown in the figure. Write the magnitudes and directions of the net fields in the regions marked II and III.
An electron beam projected along the positive x-axis deflects along the positive y-axis. If this deflection is caused by a magnetic field, what is the direction of the field? Can we conclude that the field is parallel to the z-axis?
and ```vecE` and `vecB`denote electric and magnetic fields in a frame S and `vecE`→ and `vecB` in another frame S' moving with respect to S at a velocity `vecV` Two of the following equations are wrong. Identify them.
(a) `B_y^, = B_y + (vE_z)/c^2`
(b) `E_y^' = E_y - (vB_z)/(c^2)`
`(c) Ey = By + vE_z`
`(d) E_y = E_y + vB_z`
An electron is moving along the positive x-axis. You want to apply a magnetic field for a short time so that the electron may reverse its direction and move parallel to the negative x-axis. This can be done by applying the magnetic field along
(a) y-axis
(b) z-axis
(c) y-axis only
(d) z-axis only
Two parallel, long wires carry currents i1 and i2 with i1 > i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 10 µT. If the direction of i2 is reversed, the field becomes 30 µT. The ratio i1/i2 is
A long, straight wire of radius R carries a current distributed uniformly over its cross section. T he magnitude of the magnetic field is
(a) maximum at the axis of the wire
(b) minimum at the axis of the wire
(c) maximum at the surface of the wire
(d) minimum at the surface of the wire.
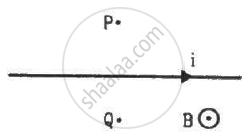
A long, straight wire carrying a current of 1.0 A is placed horizontally in a uniform magnetic field B = 1.0 × 10−5 T pointing vertically upward figure. Find the magnitude of the resultant magnetic field at the points P and Q, both situated at a distance of 2.0 cm from the wire in the same horizontal plane.
A hypothetical magnetic field existing in a region is given by `vecB = B_0 vece` where `vece`_r denotes the unit vector along the radial direction. A circular loop of radius a, carrying a current i, is placed with its plane parallel to the x−y plane and the centre at (0, 0, d). Find the magnitude of the magnetic force acting on the loop.
A straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is µ. If the wire carries a current i, what minimum magnetic field should exist in the space in order to slide the wire on the rails?
A rectangular coil of 100 turns has length 5 cm and width 4 cm. It is placed with its plane parallel to a uniform magnetic field and a current of 2 A is sent through the coil. Find the magnitude of the magnetic field B if the torque acting on the coil is 0.2 N m−1
Three coplanar parallel wires, each carrying a current of 10 A along the same direction, are placed with a separation 5.0 cm between the consecutive ones. Find the magnitude of the magnetic force per unit length acting on the wires.
Two parallel wires separated by a distance of 10 cm carry currents of 10 A and 40 A along the same direction. Where should a third current by placed so that it experiences no magnetic force?
Define Ampere in terms of force between two current carrying conductors.
Five long wires A, B, C, D and E, each carrying current I are arranged to form edges of a pentagonal prism as shown in figure. Each carries current out of the plane of paper.
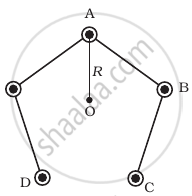
- What will be magnetic induction at a point on the axis O? AxisE is at a distance R from each wire.
- What will be the field if current in one of the wires (say A) is switched off?
- What if current in one of the wire (say) A is reversed?
Beams of electrons and protons move parallel to each other in the same direction. They ______.
Two long parallel wires kept 2 m apart carry 3A current each, in the same direction. The force per unit length on one wire due to the other is ______.
Two long straight parallel current-carrying conductors are kept ‘a’ distant apart in the air. The direction of current in both the conductors is the same. Find the magnitude of force per unit length and the direction of the force between them. Hence define one ampere.
