Advertisements
Advertisements
प्रश्न
Two molecules of a gas have speeds of 9 × 10 6 ms−1 and 1 × 106 ms−1, respectively. What is the root mean square speed of these molecules?
उत्तर
For n-molecules, we know that
`v_(rms) = sqrt((v_1^2 + v_2^2 + v_3^2 + ...... + v_n^2)/n` .....`[(v_(rms) = "root mean"),("square velocity")]`
Where v1, v2, v3 ....... vn are individual velocities of n-molecules of the gas.
For two molecules,
`v_(rms) = sqrt((v_1^2 + v_2^2)/2` ......[v1, v2, v3 ....... vn are individual velocity]
Given, `v_1 = 9 xx 10^6` m/s
And `v_2 = 1 xx 10^6` m/s
∴ `v_(rms) = sqrt(((9 xx 10^6)^2 + (1 xx 10^6)^2)/2`
= `sqrt((81 xx 10^12 + 1 xx 10^12)/2`
= `sqrt(((81 + 1) xx 10^12)/2`
= `sqrt((82 xx 10^12)/2`
= `sqrt(41) xx 10^6` m/s
APPEARS IN
संबंधित प्रश्न
Comment on the following statement: the temperature of all the molecules in a sample of a gas is the same.
Figure shows a cylindrical tube of cross-sectional area A fitted with two frictionless pistons. The pistons are connected to each other by a metallic wire. Initially, the temperature of the gas is T0 and its pressure is p0 which equals the atmospheric pressure. (a) What is the tension in the wire? (b) What will be the tension if the temperature is increased to 2T0 ?

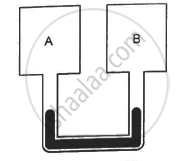
Figure shows two rigid vessels A and B, each of volume 200 cm3, containing an ideal gas (Cv = 12.5 J K−1 mol−1). The vessels are connected to a manometer tube containing mercury. The pressure in both the vessels is 75 cm of mercury and the temperature is 300 K. (a) Find the number of moles of the gas in each vessel. (b) 5.0 J of heat is supplied to the gas in vessel A and 10 J to the gas in vessel B. Assuming there's no appreciable transfer of heat from A to B, calculate the difference in the heights of mercury in the two sides of the manometer. Gas constant, R = 8.3 J K−1 mol−1.
Answer in brief:
A gas in a cylinder is at pressure P. If the masses of all the molecules are made one-third of their original value and their speeds are doubled, then find the resultant pressure.
Answer in brief:
Show that rms velocity of an oxygen molecule is `sqrt2` times that of a sulfur dioxide molecule at S.T.P.
Answer in brief:
Compare the rms speed of hydrogen molecules at 127ºC with rms speed of oxygen molecules at 27ºC given that molecular masses of hydrogen and oxygen are 2 and 32 respectively.
If the density of oxygen is 1.44 kg/m3 at a pressure of 105 N/m2, find the root mean square velocity of oxygen molecules.
Energy is emitted from a hole in an electric furnace at the rate of 20 W when the temperature of the furnace is 727°C. What is the area of the hole? (Take Stefan’s constant σ to be 5.7 × 10-8 Js-1 m-2K-4.)
Average kinetic energy of H2 molecule at 300K is 'E'. At the same temperature, average kinetic energy of O2 molecule will be ______.
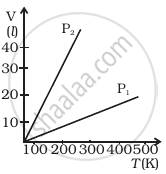
Volume versus temperature graphs for a given mass of an ideal gas are shown in figure at two different values of constant pressure. What can be inferred about relation between P1 and P2?