Advertisements
Advertisements
प्रश्न
Two parallel lines are cut by a transversal. For each pair of interior angles on the same side of the transversal, if one angle exceeds the twice of the other angle by 48°. Find the angles
उत्तर
Let the two parallel lines be m and n and l be the transversal
Let one of the interior angles on the same side of the transversal be x
Then the other will be 2x + 48°
We know that they are supplementary.
∴ x + (2x + 48°) = 180°
x + 2x + 48° = 180°
3x + 48° = 180°
3x + 48° − 48° = 180° − 48°
3x = 132°
x = `(132^circ)/3`
x = 44°
∴ One angle is x = 44°
Other angel is 2x + 48° = 2(44) + 48°
= 88 + 48°
= 136°
∴ The angles are 44° and 136°
APPEARS IN
संबंधित प्रश्न
In the figure, AB is parallel to CD, find x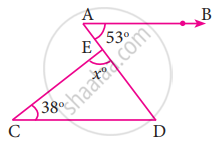
Find the measure of angle x in the following figure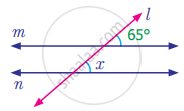
Find the measure of angle x in the following figure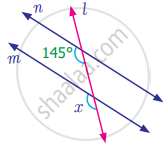
Find the measure of angle x in the following figure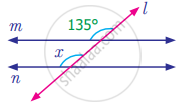
Find the value of angle x in the following figure
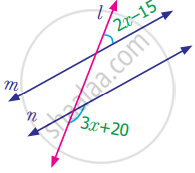
In the parking lot shown, the lines that mark the width space are parallel. If ∠1 =(x + 39)°, ∠2 = (2x – 3y)° find x and y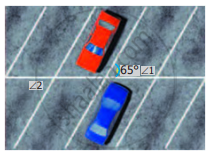
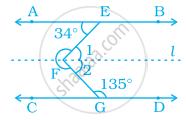
In the figure AB in parallel to CD. Find x°, y° and z°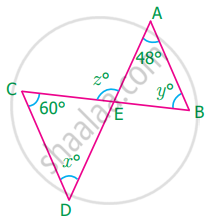
Anbu has marked the angles as shown in the following figure. Check whether it is correct. Give reason
In the given figure, l || m || n. ∠QPS = 35° and ∠QRT = 55°. Find ∠PQR.

In the given figure, AB || CD. Find the reflex ∠EFG.