Advertisements
Advertisements
प्रश्न
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m, what is the distance between their tops?
पर्याय
13 m
14 m
15 m
12.8 m
उत्तर
13 m
Explanation;
Hint: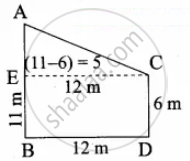
AC2 = AE2 + EC2 .....(Distance between the two tops)
= 52 + 122
= 25 + 144
= 169
AC = `sqrt(169)` = 13 cm
APPEARS IN
संबंधित प्रश्न
Sides of the triangle are 7 cm, 24 cm, and 25 cm. Determine whether the triangle is a right-angled triangle or not.
In the rectangle WXYZ, XY + YZ = 17 cm, and XZ + YW = 26 cm. Calculate the length and breadth of the rectangle?

In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. The length of the side AC is
If the sides of a triangle are in the ratio 5 : 12 : 13 then, it is ________
8, 15, 17 is a Pythagorean triplet
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
8, 15, 17
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
24, 45, 51
Choose the correct alternative:
In right angled triangle, if sum of the squares of the sides of right angle is 169, then what is the length of the hypotenuse?
A rectangle having dimensions 35 m × 12 m, then what is the length of its diagonal?
In ∆LMN, l = 5, m = 13, n = 12 then complete the activity to show that whether the given triangle is right angled triangle or not.
*(l, m, n are opposite sides of ∠L, ∠M, ∠N respectively)
Activity: In ∆LMN, l = 5, m = 13, n = `square`
∴ l2 = `square`, m2 = 169, n2 = 144.
∴ l2 + n2 = 25 + 144 = `square`
∴ `square` + l2 = m2
∴By Converse of Pythagoras theorem, ∆LMN is right angled triangle.
