Advertisements
Advertisements
प्रश्न
Two polygons of the same number of sides are similar, if (a) their corresponding angles are ______ and (b) their corresponding sides are ______. (equal, proportional)
उत्तर
Two polygons of the same number of sides are similar, if (a) their corresponding angles are equal and (b) their corresponding sides are proportional.
संबंधित प्रश्न
Give two different example of a pair of similar figures.
Give two different examples of pair of Non-similar figures.
Write the truth value (T/F) of each of the following statement
Any two similar figures are congruent.
Write the truth value (T/F) of each of the following statement
Any two congruent figures are similar.
Write the truth value (T/F) of each of the following statement
Two polygons are similar, if their corresponding sides are proportional.
Write the truth value (T/F) of each of the following statement
Two polygons are similar if their corresponding angles are proportional.
Write the truth value (T/F) of each of the following statement
Two triangles are similar if their corresponding sides are proportional.
Write the truth value (T/F) of each of the following statement
Two triangles are similar if their corresponding angles are proportional.
For each of the following statements state whether true(T) or false (F)
any two rectangles are similar
For each of the following statements state whether true(T) or false (F)
if two triangles are similar then their corresponding angles are equal and their corresponding sides are equal
If O is Any Point Inside a Rectangle Abcd Then `Oa^2+Oc^2=Ob^2+Od^2`
Similar triangles have the same ________ but not necessarily the same size
The symbol ~ is used to represent _________ triangles
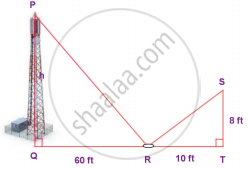
The height of a tower is measured by a mirror on the ground at R by which the top of the tower’s reflection is seen. Find the height of the tower. If ∆PQR ~ ∆STR
If in two As ABC and DEF, `"AB"/"DF" = "BC"/"FE" = "CA"/"ED"`, then ______.
Given below is the picture of the Olympic rings made by taking five congruent circles of radius 1cm each, intersecting in such a way that the chord formed by joining the point of intersection of two circles is also of length 1cm. Total area of all the dotted regions assuming the thickness of the rings to be negligible is ______.

The lengths of the diagonals of a rhombus are 16 cm and 12 cm. Then, the length of the side of the rhombus is ______.
In Figure, ∠BAC = 90° and AD ⊥ BC. Then, ______.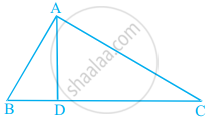
Observe the figures given below carefully and answer the questions:
| Figure A | 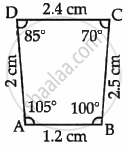 |
 |
| Figure B |  |
 |
| Figure C | 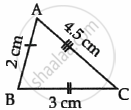 |
 |
- Name the figure(s) where in two figures are similar.
- Name the figure(s) where in the figures are congruent.
-
- Prove that congruent triangles are also similar but not the converse.
OR - What more is least needed for two similar triangles to be congruent?
- Prove that congruent triangles are also similar but not the converse.
