Advertisements
Advertisements
प्रश्न
Two small bodies of masses 10 kg and 20 kg are kept a distance 1.0 m apart and released. Assuming that only mutual gravitational forces are acting, find the speeds of the particles when the separation decreases to 0.5 m.
उत्तर
Consider a system of two bodies. The initial linear momentum of the system is zero as the bodies were initially at rest when they were released.
Since the gravitational force is an internal force and the net external force on the system is zero, so by the law of conservation of linear momentum, the final momentum of the system will also be zero.
So, 10 \[\times\] v1 = 20 \[\times\] v2
⇒ v1 = 2 v2 ...(i)
Applying the law of conservation of energy,We have;
nitial total energy = final total energy ...(ii)
Initial total energy \[= \frac{- 6 . 67 \times {10}^{11} \times 10 \times 20}{1}\] + 0
= −13.34 × 10−9 J ...(iii)
When the separation is 0.5 m, we have:
Final total energy \[= \frac{- 13 . 34 \times {10}^{- 9}}{1/2} + \left( \frac{1}{2} \right) \times 10 v_1^2 + \left( \frac{1}{2} \right) \times 20 v_2^2 . . . \left( iv \right)\]
From (iii) and (iv), we have:
−13.34 × 10−9 = 26.68 × 10−9 + \[5 v_1^2 + 10 v_2^2\]
⇒−13.34 × 10−9 = 26.68 + 10−9 + \[30 v_2^2\]
\[\Rightarrow v_2^2 = \frac{- 13 . 34 \times {10}^{- 9}}{30}\] = 4.44 × 10−10
⇒ v2 = 2.1 × 10−5 m/s
∴ v1 = 4.2 × 10−5 m/s
APPEARS IN
संबंधित प्रश्न
What is the importance of the universal law of gravitation?
How will you ‘weigh the sun’, that is estimate its mass? The mean orbital radius of the earth around the sun is 1.5 × 108 km.
State Kepler’s law which is represented by the relation r3 ∝ T2.
State and explain Kepler's laws of planetary motion. Draw diagrams to illustrate these laws.
Can you think of two particles which do not exert gravitational force on each other?
The weight of an object is more at the poles than at the equator. Is it beneficial to purchase goods at equator and sell them at the pole? Does it matter whether a spring balance is used or an equal-beam balance is used?
Consider a planet moving in an elliptical orbit round the sun. The work done on the planet by the gravitational force of the sun
(a) is zero in any small part of the orbit
(b) is zero in some parts of the orbit
(c) is zero in one complete revolution
(d) is zero in no part of the motion.
Two spherical balls of mass 10 kg each are placed 10 cm apart. Find the gravitational force of attraction between them.
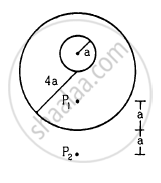
A uniform metal sphere of radius a and mass M is surrounded by a thin uniform spherical shell of equal mass and radius 4a (In the following figure). The centre of the shell falls on the surface of the inner sphere. Find the gravitational field at the points P1 and P2 shown in the figure.
The gravitational field in a region is given by \[E = \left( 2 \overrightarrow{i} + 3 \overrightarrow{j} \right) N {kg}^{- 1}\] . Show that no work is done by the gravitational field when a particle is moved on the line 3y + 2x = 5.
[Hint : If a line y = mx + c makes angle θ with the X-axis, m = tan θ.]
The acceleration produced by a force in an object is directly proportional to the applied _________ And inversely proportional to the _________ Of the object.
How will the force of gravitation between two objects change if the distance between them is:
Halved
How will the force of gravitation between two objects change if the distance between them is:
Almost zero
A ball is thrown up with a speed of 4.9 ms-1.
Prove that the time of ascent is equal to the time of descent.
What does a force do in the following case?
You apply brakes to a running car.
Name and state the action and reaction in the following case:
A book lying on a table.
Why does a ball moving on a table top eventually stops?
Is there a gravitational attraction between you and the book? Explain.
The distance-time values for an object moving along straight line are given below:
| Time (s) | Distance (m) |
| 0 | 0 |
| 1 | 1 |
| 2 | 8 |
| 3 | 27 |
Answer the following question.
What are the dimensions of the universal gravitational constant?
