Advertisements
Advertisements
प्रश्न
Using division of polynomials, state whether
x + 6 is a factor of x2 − x − 42
उत्तर
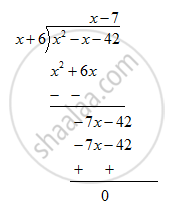
Remainder is zero. Hence (x+6) is a factor of x2 -x-42
APPEARS IN
संबंधित प्रश्न
Divide the given polynomial by the given monomial.
(3y8 − 4y6 + 5y4) ÷ y4
Write the degree of each of the following polynomials.
Divide 15m2n3 by 5m2n2.
Divide 4y2 + 3y +\[\frac{1}{2}\] by 2y + 1.
Divide 6x3 + 11x2 − 39x − 65 by 3x2 + 13x + 13 and find the quotient and remainder.
Divide 30x4 + 11x3 − 82x2 − 12x + 48 by 3x2 + 2x − 4 and find the quotient and remainder.
Verify the division algorithm i.e. Dividend = Divisor × Quotient + Remainder, in each of the following. Also, write the quotient and remainder.
| Dividend | Divisor |
| 34x − 22x3 − 12x4 − 10x2 − 75 | 3x + 7 |
Verify the division algorithm i.e. Dividend = Divisor × Quotient + Remainder, in each of the following. Also, write the quotient and remainder.
| Dividend | Divisor |
| 4y3 + 8y + 8y2 + 7 | 2y2 − y + 1 |
Find whether the first polynomial is a factor of the second.
4y + 1, 8y2 − 2y + 1
Statement A: If 24p2q is divided by 3pq, then the quotient is 8p.
Statement B: Simplification of `((5x + 5))/5` is 5x
