Advertisements
Advertisements
प्रश्न
Using division of polynomials, state whether
4x − 1 is a factor of 4x2 − 13x − 12
उत्तर
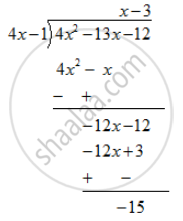
As the remainder is non zero . Hence ( 4x-1) is not a factor of 4x2 -13x-12
APPEARS IN
संबंधित प्रश्न
Write the degree of each of the following polynomials.
Write the degree of each of the following polynomials.
Write each of the following polynomials in the standard form. Also, write their degree.
(x3 − 1)(x3 − 4)
Write each of the following polynomials in the standard form. Also, write their degree.
Simplify:\[\frac{32 m^2 n^3 p^2}{4mnp}\]
Divide\[- x^6 + 2 x^4 + 4 x^3 + 2 x^2\ \text{by} \sqrt{2} x^2\]
Verify the division algorithm i.e. Dividend = Divisor × Quotient + Remainder, in each of the following. Also, write the quotient and remainder.
| Dividend | Divisor |
| 34x − 22x3 − 12x4 − 10x2 − 75 | 3x + 7 |
Simplify `(14"p"^5"q"^3)/(2"p"^2"q") - (12"p"^3"q"^4)/(3"q"^2)`
Divide: 81(p4q2r3 + 2p3q3r2 – 5p2q2r2) by (3pqr)2
The denominator of a fraction exceeds Its numerator by 8. If the numerator is increased by 17 and the denominator is decreased by 1, we get `3/2`. Find the original fraction.
