Advertisements
Advertisements
प्रश्न
Using Huygen's wave theory of light, show that the angle of incidence is equal to the angle of reflection. Draw a neat and labelled diagram.
उत्तर
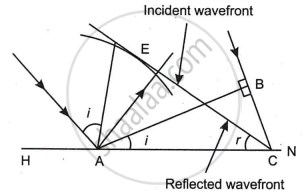
Consider a plane wave AB incident at an angle i on a reflecting surface MN. If v represents the speed of the wave in the medium and if T represents the time taken by the wavefront to advance from point B to C, then distance BC = vt.
In order to construct the reflected wavefront, a sphere of radius = vt is drawn from point A, as shown in the figure. Let CE represent the tangent plane drawn from the point C to this surface.
∴ AE = BC = vt
∠ABC = ∠CEA = 90°
Here AC is common.
∴ ΔEAC ≅ ΔBAC
Hence i = r.
APPEARS IN
संबंधित प्रश्न
Explain the construction of plane wavefront using Huygens’ principle.
You have learnt in the text how Huygens’ principle leads to the laws of reflection and refraction. Use the same principle to deduce directly that a point object placed in front of a plane mirror produces a virtual image whose distance from the mirror is equal to the object distance from the mirror.
Consider a plane wave front incident on a thin convex lens. Draw a proper diagram to show how the incident wave front traverses through the lens and after refraction focusses on the focal point of the lens, giving the shape of the emergent wave front.
Use Huygens' principle to verify the laws of refraction.
The refractive indices of water and diamond are `4/3` and 2.42 respectively. Find the speed of light in water and diamond. (c = 3x108 m/s)
Define a wavefront. Using 'Huygens' principle, draw the shape of a refracted wavefront, when a plane wave is incident on a convex lens.
Wavefront means
For light diverging from a point source ______.
- the wavefront is spherical.
- the intensity decreases in proportion to the distance squared.
- the wavefront is parabolic.
- the intensity at the wavefront does not depend on the distance.
What type of wavefronts are associated with a point source of light?
Represent diagrammatically how the incident planar wavefronts of wavelength λ pass through an aperture of size d, when d is approximately equal to λ.
