Advertisements
Advertisements
प्रश्न
Using the Reminder Theorem, factorise of the following completely.
2x3 + x2 – 13x + 6
उत्तर
Let f (x) = 2x3 + x2 − 13x + 6
For x = 2,
f(x) = f(2) = 2(2)3 + (2)2 − 13(2) + 6 = 16 + 4 − 26 + 6 = 0
Hence, (x − 2) is a factor of f(x).
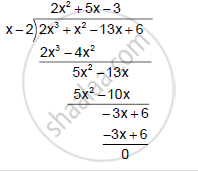
∴ `2x^3 + x^2 - 13x + 6 = (x-2) (2x^2 + 5x -3)`
= `(x-2)(2x^2 + 6x -x -3)`
= `(x-2) [2x(x + 3) -(x-3)]`
=` (x - 2)(x + 3) (2x - 1)`
APPEARS IN
संबंधित प्रश्न
Using the Remainder Theorem, factorise each of the following completely.
3x3 + 2x2 – 23x – 30
Find the number that must be subtracted from the polynomial 3y3 + y2 – 22y + 15, so that the resulting polynomial is completely divisible by y + 3.
Using Remainder Theorem, factorise : x3 + 10x2 – 37x + 26 completely.
Factorise x3 + 6x2 + 11x + 6 completely using factor theorem.
The polynomial px3 + 4x2 – 3x + q is completely divisible by x2 – 1; find the values of p and q. Also, for these values of p and q, factorize the given polynomial completely.
Using remainder Theorem, factorise:
2x3 + 7x2 − 8x – 28 Completely
Find the value of a and b so that the polynomial x3 - ax2 - 13x + b has (x - 1) (x + 3) as factor.
If x – 2 is a factor of each of the following three polynomials. Find the value of ‘a’ in each case:
x3 + 2ax2 + ax - 1
If (x + 3) and (x – 4) are factors of x3 + ax2 – bx + 24, find the values of a and b: With these values of a and b, factorise the given expression.
Factorize completely using factor theorem:
2x3 – x2 – 13x – 6
