Advertisements
Advertisements
Question
Using the Reminder Theorem, factorise of the following completely.
2x3 + x2 – 13x + 6
Solution
Let f (x) = 2x3 + x2 − 13x + 6
For x = 2,
f(x) = f(2) = 2(2)3 + (2)2 − 13(2) + 6 = 16 + 4 − 26 + 6 = 0
Hence, (x − 2) is a factor of f(x).
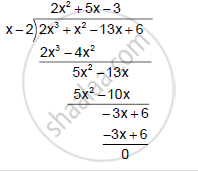
∴ `2x^3 + x^2 - 13x + 6 = (x-2) (2x^2 + 5x -3)`
= `(x-2)(2x^2 + 6x -x -3)`
= `(x-2) [2x(x + 3) -(x-3)]`
=` (x - 2)(x + 3) (2x - 1)`
APPEARS IN
RELATED QUESTIONS
A two digit positive number is such that the product of its digits is 6. If 9 is added to the number, the digits interchange their places. Find the number.
When divided by x – 3 the polynomials x3 – px2 + x + 6 and 2x3 – x2 – (p + 3) x – 6 leave the same remainder. Find the value of ‘p’.
Given that x – 2 and x + 1 are factors of f(x) = x3 + 3x2 + ax + b; calculate the values of a and b. Hence, find all the factors of f(x).
In the following two polynomials, find the value of ‘a’ if x – a is a factor of each of the two:
x5 - a2x3 + 2x + a + 1.
If x – 2 is a factor of each of the following three polynomials. Find the value of ‘a’ in each case:
x5 - 3x4 - ax3 + 3ax2 + 2ax + 4.
Show that x2 - 9 is factor of x3 + 5x2 - 9x - 45.
The polynomial 3x3 + 8x2 – 15x + k has (x – 1) as a factor. Find the value of k. Hence factorize the resulting polynomial completely.
One factor of x3 – kx2 + 11x – 6 is x – 1. The value of k is ______.
For the polynomial x5 – x4 + x3 – 8x2 + 6x + 15, the maximum number of linear factors is ______.
If f(x) = 3x + 8; the value of f(x) + f(– x) is ______.
