Advertisements
Advertisements
प्रश्न
Using ruler and compasses only, construct a triangle ABC in which AB=S cm, BC=6 cm and CA=4.5 cm. Construct a circle passing through A, Band c.
उत्तर
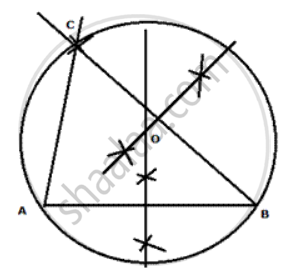
Steps of Construction:
(i) Draw line AB = S cm
(ii) At B, draw an arc with radius 6 cm
(iii) On the arc cut AC = 4.5 cm.
(iv) Join AC and BC.
(v) Draw perpendicular bisectors of AB and BC, which meet at O.
(vi) With O as centre and radius equal to the distance between O and the vertex of the triangle, draw a circle to pass through alI the three vertices of the triangle. (vii) The circle drawn is the required circle.
APPEARS IN
संबंधित प्रश्न
Construct a regular hexagon of side 5 cm. Hence construct all its lines of symmetry and name them.
Using ruler and compass only, construct a ΔABC such that BC = 5 cm and AB = 6.5
cm and ∠ABC = 120°
1) Construct a circum-circle of ΔABC
2) Construct a cyclic quadrilateral ABCD, such that D is equidistant from AB and BC.
In the figure given below 'O' is the centre of the circle. If QR = OP and ∠ORP = 20°. Find the value of 'x' giving reasons

Using ruler and compasses only,
- Construct a triangle ABC with the following data :
Base AB = 6 cm, BC = 6.2 cm and ∠CAB = 60°. - In the same diagram, draw a circle which passes through the points A, B and C and mark its center O.
- Draw a perpendicular from O to AB which meets AB in D.
- Prove that : AD = BD.
Contruct a ΔABC with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the incircle of the triangle. Measure and record the radius of the incricle.
Draw a circle of radius 2. 5 cm and circumscribe a square about it.
Draw a circle of radius 4.5 cm. Take a point Pon its circumference. Construct a tangent to the circle at P without using the centre.
Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
What is the relation between the distances OA, OB and OC?
Use ruler and compasses only for this question:
(i) Construct A ABC, where AB = 3.5 cm, BC = 6 cm and ∠ ABC = 60°.
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark the point P which is equidistant from AB, BC, and also equidistant from B and C. Measure and record the length of PB.
Ruler and compasses only may be used in this question. All constructions lines and arcs must be clearly shown, and the be sufficient length and clarity to permit assessment:
(i) Construct a triangle ABC, in which AB = 9 cm, BC = 10 cm and angle ABC = 45°.
(ii) Draw a circle, with center A and radius 2.5 cm. Let it meet AB at D.
(iii) Construct a circle to touch the circle with center A externally at D and also to touch the line BC.
