Advertisements
Advertisements
प्रश्न
What least number must be subtracted from each of the numbers 7, 17 and 47 so that the remainders are in continued proportion?
उत्तर
Let the number subtracted be x.
∴ (7 – x) : (17 – x) :: (17 – x)(47 – x)
`(7 - x)/(17 - x) = (17 - x)/(47 - x)`
(7 – x)(46 – x) = (17 – x)2
329 – 47x – 7x + x2 = 289 – 34x + x2
329 – 289 = –34x + 54x
20x = 40
x = 2
Thus, the required number which should be subtracted is 2.
APPEARS IN
संबंधित प्रश्न
If x + 5 is the mean proportional between x + 2 and x + 9; find the value of x.
Using properties of proportion, solve for x:
`(3x + sqrt(9x^2 - 5))/(3x - sqrt(9x^2 - 5)) = 5`
Find the third proportional to 0.24, 0.6
Write (T) for true and (F) for false in case of the following:
81 kg : 45 kg : : 18 men : 10 men
If `x/a = y/b = z/c`, prove that `[(a^2x^2 + b^2y^2 + c^2z^2)/(a^2x + b^3y +c^3z)]^3 = "xyz"/"abc"`
The shadow of a 3 m long stick is 4m long. At the same time of the day, if the shadow of a flagstaff is 24 m long, how tall is the flagstaff?
Unequal masses will not balance on a fulcrum if they are at equal distance from it; one side will go up and the other side will go down.
Unequal masses will balance when the following proportion is true:
`("mass"1)/("length"2) = ("mass"2)/("length"1)`
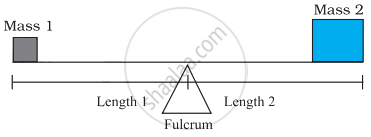
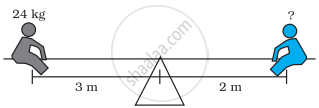
Two children can be balanced on a seesaw when
`("mass"1)/("length"2) = ("mass"2)/("length"1)`. The child on the left and child on the right are balanced. What is the mass of the child on the right?
The mean proportional between 4 and 9 is ______.
If `(a + b)^3/(a - b)^3 = 64/27`.
- Find `(a + b)/(a - b)`
- Hence using properties of proportion, find a : b.
The table, given below, shows the values of x and y, where x is proportional (directly proportional) to y.
| x | A | 24 | 15 |
| y | 12 | B | 20 |
The values of A and B are:
