Advertisements
Advertisements
प्रश्न
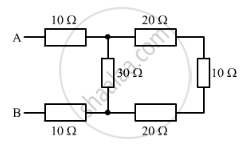
उत्तर
The resistors of values 20 Ω, 10 Ω and 20 Ω are connected in series. Therefore, their net resistance is:
R = 20 Ω + 10 Ω + 20 Ω
R = 50 Ω
This combination of resistors are connected in parallel with that of value 30 Ω. Therefore, the resistance R' is:
1/R' = (1/50) + (1/30)
1/R' = (3 + 5)/150
R' = 150/8
R' = 18.75 Ω
The resistance, R' is connected in series with the two resistors of values 10 Ω each. Hence, the total resistance between A and B is:
18.75 + 10 + 10 = 38.75 Ω
APPEARS IN
संबंधित प्रश्न
Write down an expression for the resistance of a metallic wire in terms of the resistivity.
Give the law of combination of resistances in series.
You are supplied with a number of 100 Ω resistors. How could you combine some of these resistors to make a 250 Ω resistor?
What potential difference is needed to drive a current o f 1 A through a 5 Ω resistor?
How does the resistivity of a semiconductor depend on temperature?
State expression for Resistance connected in parallel.
Four resistances of 2.0Ω each are joined end to end, to form a square ABCD. Calculate the equivalent resistance of the combination between any two adjacent comers.
Illustrate-combination of cells e.g., three cells, in series, explaining the combination briefly. Obtain an expression for current ‘i’ in the combination.
Show how you would connect three resistors, each of resistance 6 Ω, so that the combination has a resistance of 4 Ω.
