Advertisements
Advertisements
प्रश्न
What is (a) highest, and (b)Ω lowest, resistance which can be obtained by combining four resistors having the following resistances?
4 Ω, 8 Ω, 12 Ω, 24 Ω
Advertisements
उत्तर
(a) To get the highest resistance, all the resistors must be connected in series.
Resistance in a series arrangement is given by R = R1+ R2 + R3 + R4
R=4Ω+8Ω+12Ω+24Ω
R=48Ω
Therefore, the highest resistance is 48 Ω.
(b) To get the lowest resistance, all the resistors must be connected in parallel.
Resistance in a parallel arrangement is given by:
`1/R=1/R_1+1/R_2+1/R_3+1/R_4`
Here`R_1=4`Ω
`R_2=8` Ω
`R_3=12` Ω
`R_4=24`Ω
`1/R=1/4+1/8+1/12+1/24`
`1/R=(6+3+2+1)/24`
`1/R=12/24`
R=2Ω
Therefore, the lowest resistance of the arrangement is 2 Ω.
APPEARS IN
संबंधित प्रश्न
A piece of wire of resistance R is cut into five equal parts. These parts are then connected in parallel. If the equivalent resistance of this combination is R’, then the ratio `"R"/"R'"` is ______.
Find the equivalent resistance between points A and B.
An electrical appliance has a resistance of 25 Ω. When this electrical appliance is connected to a 230 V supply line, the current passing through it will be:
(a) 0.92 A
(b) 2.9 A
(c) 9.2 A
(d) 92 A
Name the material which is the best conductor of electricity.
How does the resistance of a wire change when:
its diameter is tripled?
Give the law of combination of resistances in series.
If five resistances, each of value 0.2 ohm, are connected in series, what will be the resultant resistance?
V = IRTwo resistances X and Y are connected turn by turn : (i) in parallel, and (ii) series. In which case the resultant resistance will be less than either of the individual resistances?R = R1+ R2+ R3
Calculate the combined resistance in each case:
Name a substance of which the resistance remains almost unchanged by the increase in temperature.
State how are the two resistors joined with a battery when equivalent resistance is more than either of the two resistances.
What potential difference is needed to drive a current o f 1 A through a 5 Ω resistor?
State a relation between electrical power, resistance and potential difference in an electrical circuit.
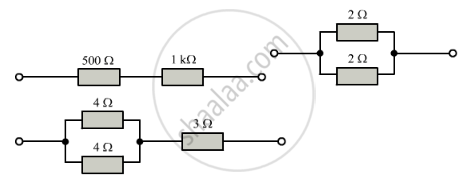
Calculate the equivalent resistance between P and Q from the following diagram:
Illustrate-combination of cells e.g., three cells, in series, explaining the combination briefly. Obtain an expression for current ‘i’ in the combination.
Illustrate-combination of cells e.g., three cells, in parallel, explaining the combination briefly. Obtain an expression for current ‘i’ in the combination.
If R1 and R2 be the resistance of the filament of 40 W and 60 W respectively operating 220 V, then:
Two electric bulbs have resistances in the ratio 1 : 2. If they are joined in series, the energy consumed in them is in the ratio:
Show how you would connect three resistors, each of resistance 6 Ω, so that the combination has a resistance of 4 Ω.
