Advertisements
Advertisements
प्रश्न
Which term of the Arithmetic Progression (A.P.) 15, 30, 45, 60...... is 300?
Hence find the sum of all the terms of the Arithmetic Progression (A.P.)
उत्तर
Given A.P. is 15, 30, 45, 60.........
Here a = 15, d = 30 – 15 = 15
Let Tn = 300
Tn = a + (n – 1)d
300 = 15 + (n – 1) × 15
300 = 15 + 15n – 15
15n = 300
∴ n = 20
Hence, 300 is the 20th term
Also by Sn = `n/2 [2a + (n - 1)d]`
S20 = `20/2 [2 xx 15 + (20 - 1) xx 15]`
= 10[30 + 285]
= 10 × 315
∴ S20 = 3150
APPEARS IN
संबंधित प्रश्न
In a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant will be the same as the class, in which they are studying, e.g., a section of class I will plant 1 tree, a section of class II will plant 2 trees, and so on till class XII. There are three sections of each class. How many trees will be planted by the students?
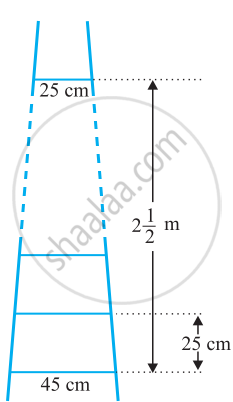
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
Find the sum to n term of the A.P. 5, 2, −1, −4, −7, ...,
Find the sum 3 + 11 + 19 + ... + 803
Find the value of x for which (x + 2), 2x, ()2x + 3) are three consecutive terms of an AP.
Write an A.P. whose first term is a and common difference is d in the following.
a = 6, d = –3
The sum of the first n terms of an A.P. is 3n2 + 6n. Find the nth term of this A.P.
The sum of the first three terms of an Arithmetic Progression (A.P.) is 42 and the product of the first and third term is 52. Find the first term and the common difference.
Which term of the AP: –2, –7, –12,... will be –77? Find the sum of this AP upto the term –77.
If Sn denotes the sum of first n terms of an AP, prove that S12 = 3(S8 – S4)
