Advertisements
Advertisements
प्रश्न
Write 5th term from the end of the A.P. 3, 5, 7, 9, ..., 201.
उत्तर
In the given problem, we need to find the 5th term from the end for the given A.P.
3, 5, 7, 9 …201
Here, to find the 5th term from the end let us first find the common difference of the A.P. So,
First term (a) = 3
Last term (an) = 201
Common difference (d) = 5 - 3 = 2
Now, as we know, the nth term from the end can be given by the formula,
an = l - (n-1) d
So, the 5th term from the end,
a5 = 201 - (5-1)2
= 201 - (4)2
= 201 - 8
= 193
Therefore, the 5th term from the end of the given A.P. is 193 .
APPEARS IN
संबंधित प्रश्न
If the sum of the first n terms of an AP is 4n − n2, what is the first term (that is, S1)? What is the sum of the first two terms? What is the second term? Similarly, find the 3rd, the 10th, and the nth terms.
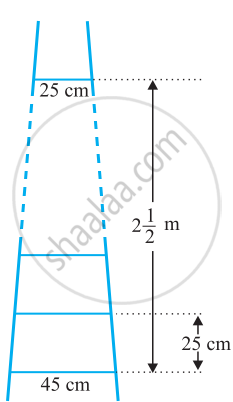
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
If (m + 1)th term of an A.P is twice the (n + 1)th term, prove that (3m + 1)th term is twice the (m + n + 1)th term.
Find the sum of all even integers between 101 and 999.
Find the sum of all natural numbers between 250 and 1000 which are divisible by 9.
Which term of AP 72,68,64,60,… is 0?
What is the 5th term form the end of the AP 2, 7, 12, …., 47?
Find the sum of all multiples of 9 lying between 300 and 700.
If the sum of first n even natural numbers is equal to k times the sum of first n odd natural numbers, then k =
Which term of the Arithmetic Progression (A.P.) 15, 30, 45, 60...... is 300?
Hence find the sum of all the terms of the Arithmetic Progression (A.P.)
