Advertisements
Advertisements
प्रश्न
ΔXYZ की रचना कीजिए जिसमें XY + XZ = 10.3 सेमी, YZ = 4.9 सेमी, `angle`XYZ = 45°
उत्तर
कच्ची आकृति:
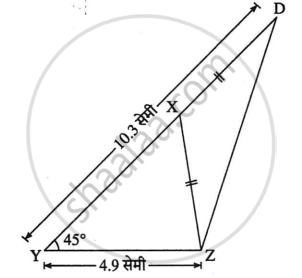
स्पष्टीकरण:
कच्ची आकृति में दिखाए अनुसार, YZ = 4.9 सेमी लंबाईवाला रेखाखंड खींचिए।
रेखाखंड YZ के बिंदु Y से 45° का कोण बनाने वाले किरण पर बिंदु D इस प्रकार लें कि YD = XY + XZ = 10.3 सेमी
अब, YX + XD = YD .....[Y-X-D]
∴ YX + XD = 10.3 सेमी ....(i)
दिया हुआ, XY + XZ = 10.3 सेमी ....(ii)
∴ YX + XD = XY + XZ ....[(i) और (ii) से]
⇒ XD = XZ
बिंदु X, बिंदुओं D तथा Z से समदूरस्थ है।
बिंदु X यह रेख YD के लंबसमद्विभाजक पर स्थित है।
रेख YX तथा रेख DZ के लंबसमद्विभाजक परस्पर बिंदु X पर प्रतिच्छेदन करते है।
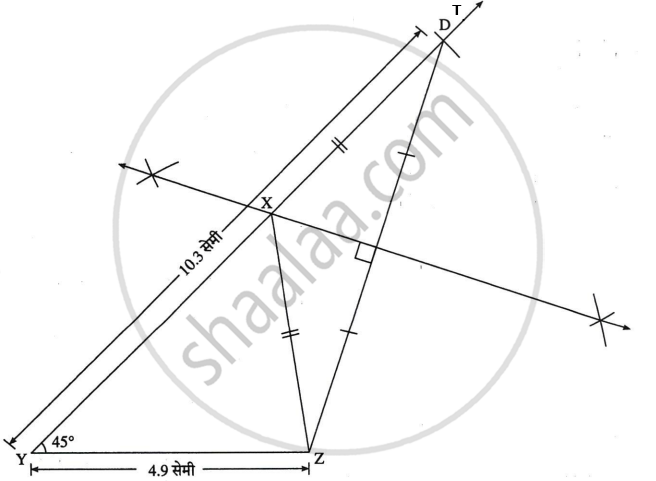
रचना के सोपान:
- 4.9 सेमी लंबाईवाली रेख YZ खींचें।
- बिंदु Y से 45° का कोण बनाने वाली किरण YT खींचिए।
- किरण YT पर बिंदु D इस प्रकार लीजिए कि d (Y, D) = 10.3 सेमी।
- रेख DZ खींचिए।
- रेख DZ का लंबसमद्विभाजक खींचो, जो किरण YT को बिंदु X पर प्रतिच्छेदित करे।
- रेख XZ खींचिए।
ΔXYZ यह अभीष्ट त्रिभुज है।
APPEARS IN
संबंधित प्रश्न
`\triangle`PQR की रचना ऐसी कीजिए जिसका आधार QR = 4.2 सेमी, m`\angle`Q = 40° तथा PQ + PR = 8.5 सेमी.
ΔXYZ की रचना ऐसी कीजिए जिसका आधार YZ = 6 सेमी, XY + XZ = 9 सेमी m`angle`XYZ = 50°
ΔABC की रचना ऐसी कीजिए जिसका आधार BC = 6.2 सेमी, m`angle`ACB = 50°, AB + AC = 9.8 सेमी
ΔABC की रचना ऐसी कीजिए जिसका आधार BC = 3.2 सेमी, `angle`ACB = 45° तथा ΔABC की परिमिति 10 सेमी हो।
