Advertisements
Advertisements
प्रश्न
यदि चतुर्भुज ABCD के ∠A और ∠B के समद्विभाजक परस्पर P पर प्रतिच्छेद करते हैं, ∠B और ∠C के समद्विभाजक Q पर, ∠C और ∠D के R पर तथा ∠D और ∠A के S पर प्रतिच्छेद करते हैं, तो PQRS है एक ______।
पर्याय
आयत
समचतुर्भुज
समांतर चतुर्भुज
चतुर्भुज जिसके सम्मुख कोण संपूरक हैं।
उत्तर
यदि चतुर्भुज ABCD के ∠A और ∠B के समद्विभाजक परस्पर P पर प्रतिच्छेद करते हैं, ∠B और ∠C के समद्विभाजक Q पर, ∠C और ∠D के R पर तथा ∠D और ∠A के S पर प्रतिच्छेद करते हैं, तो PQRS है एक चतुर्भुज जिसके सम्मुख कोण संपूरक हैं।
स्पष्टीकरण -
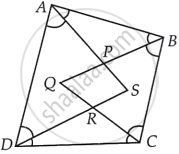
चतुर्भुज के सभी कोणों का योग 360° होता है।
⇒ ∠A + ∠B + ∠C + ∠D = 360°
दोनों पक्षों को 2 से भाग देने पर,
⇒ `1/2` (∠A + ∠B + ∠C + ∠D) = `1/2` × 360° = 180°
∵ AP, PB, RC और RD, ∠A, ∠B, ∠C और ∠D के समद्विभाजक हैं।
⇒ ∠PAB + ∠ABP + ∠RCD + ∠RDC = 180° ...(1)
त्रिभुज के सभी कोणों का योग 180° होता है।
∴ ∠PAB + ∠APB + ∠ABP = 180°
⇒ ∠PAB + ∠ABP = 180° – ∠APB ...(2)
इसी प्रकार,
∴ ∠RDC + ∠RCD + ∠CRD = 180°
⇒ ∠RDC + ∠RCD = 180° – ∠CRD ...(3)
(ii) और (iii) को (i) में प्रतिस्थापित करने पर, हम पाते हैं।
180° – ∠APB + 180° – ∠CRD = 180°
⇒ 360° – ∠APB – ∠CRD = 180°
⇒ ∠APB + ∠CRD = 360° – 180°
⇒ ∠APB + ∠CRD = 180° ...(4)
अभी,
∠SPQ = ∠APB .....[ऊर्ध्वाधर सम्मुख कोण]
∠SRQ = ∠DRC ......[ऊर्ध्वाधर विपरीत कोण]
(4) आवेदन करने पर,
⇒ ∠SPQ + ∠SRQ = 180°
APPEARS IN
संबंधित प्रश्न
एक आयत का एक विकर्ण उसकी एक भुजा से 25° पर नत है। इसके विकर्णों के बीच का न्यून कोण है
एक चतुर्भुज की रचना की जा सकती है, यदि उसके चारों कोण और एक भुजा दी हो।
7 बजे एक घड़ी की घंटे तथा मिनट की सूइयों के बीच कोणों में से छोटे कोण का माप लिखिए साथ ही, अन्य कोण का माप भी लिखिए तथा यह भी बताइए कि ये कोण किस प्रकार के हैं?
9 बजे घड़ी की घंटे तथा मिनट की सूइयों के बीच में बने कोणों के माप हैं:
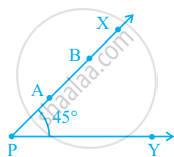
आकृति में, यदि बिंदु A को किरण PX के अनुदिश B बिंदु B पर इस प्रकार विस्थापित किया कि PB = 2PA,
तो ∠BPY का माप है-
यदि दो कोणों का योग एक अधिक कोण के बराबर है, तो निम्नलिखित में से कौन-सा विकल्प संभव नहीं है?
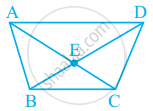
आकृति में, AE + EC क्या है?
आकृति के भाग में, दी हुई सूचना का प्रयोग करके समकोण लिखिए-
AC ⊥ BD
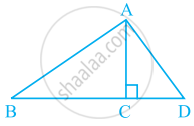
आकृति के भाग में, दी हुई सूचना का प्रयोग करके समकोण लिखिए-
AC ⊥ BD
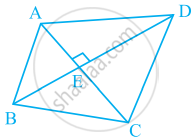
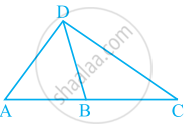
आकृति के भाग से क्या निष्कर्ष निकाला जा सकता है, यदि DB कोण ADC का समद्धिभाजक है?